異材界面における熱応力場
| Thermal Stress Field at the Interface Edge in Dissimilar Materials | ||
| In elastic dissimilar materials joint subjected to cooling or heating, thermal stresses at the intersection of the edges and the interface are singular. For the Cu/Si3N4 composite, the relation between the intensity Khj of the stress field and bonded wedge angle was examined in detail. The simultaneous equation can be represented in a matrix form as follows: [⊿}{ω}={L} where ⊿ is the coeffisient matrix of an 8×8 system, and ω and L are the vector ω={a1,b1,c1,d1,a2,b2,c2,d2}T and L={0,0,0,0,T12,0,0,0}T. Furthermore, a funstion T12 is determined from interface condition for the r direction desplacement through the Mellin transform, defined as 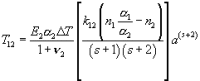 where E2(=2G2(1+ν2)) is Young's modulus of material 2 and k12 is the stiffness ratio G1/G2. And all the stress intensities can be written as 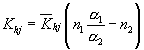 where the function  is independent of thermal expansion coefficient.Model for a two-phase bonded structure with φ1+φ2=360°is shown in figure right. Variations of wedge angle φ1 of material 1 verses Dundurs parameter α12 and stiffness ratio k12, in which Khg associated with a logarithmic singularity becomes zero, under φ1+φ2=360. |
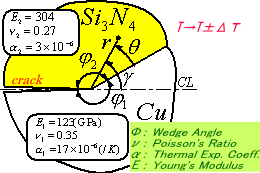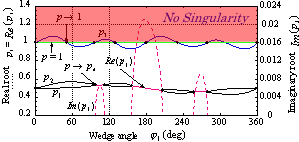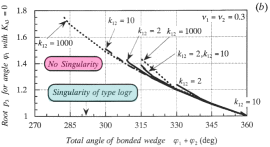   For the case where the total wedge angle is 360°, the bonded wedge angle yielding Khj=0 does not disappear, and that approaches φ1=0°as k12→∞ and φ1=360°as k12→0. For the corresponding root p3, it is found the figure above that the stress intensity Khj for singular solution of type log r is zero in the case of φ1+φ2=360°and Kh3 for the no singularity solution is zero in the cases of the other total angles, i.e., φ1+φ2  360°. That is, the singularity of type rp-1 corresponding to the third root p3 cannot disappear from the stress intensity Kh3. |
|
