解析の基礎

解析の基礎

• 1．インピーダンスの基礎
• 2．実例（コンデンサーのインピーダンス）
• 3．経験則パラメータの意味（デバイの経験則スペクトルを例に）
• 4．複素非線形最小二乗法
• 5．pyZwxで実装した重み付け
• 6．等価回路
• 7. インピーダンスのデータ構造とグラフ表示
• 8. インピーダンスと複素誘電率

1．インピーダンスの基礎

インピーダンスはO. Heaviside（1850-1925）により定義された物理量で，語源はimpede（遅らせる．邪魔する）である．抵抗（resistance）との違いは波形信号の世界において定義された物理量ということだろう．波形信号の世界とは現代的に表現するならばフーリエ領域と同意である．インピーダンス，時間領域，ラプラス領域，フーリエ領域の関係についてはD. D. Macdonaldの総説でコンパクトにまとめられている．インピーダンスはビクトリア王朝時代，大陸間海底電話線を伝搬してきた信号が入力信号と異なる波形になってしまうことを説明するために生み出された概念の一つである．（この時代オシロスコープはまだ開発されていなかったことも注目して欲しい．波形の変化を視覚的なグラフで捉えることなく理論のみで正しく理解したのだ）応答信号が入力信号と異なるのは，応答信号の変動が少なくとも時間に対する線形微積分方程式で与えられることを意味する．

ヘヴィサイドは微積分演算子法をやや荒々しく用いていたため，下記のラプラス変換，フーリエ変換とは異なる方法のように見える．ラプラス領域，フーリエ領域の解釈は後にヘヴィサイドの後に構築されたが，両者は等価であることが解っている．

ラプラス変換，ヘヴィサイド変換，フーリエ変換を簡単に復習しよう（橋本洋志他「Scilabで学ぶシステム制御の基礎」オーム社参照）．
$t < 0$で$f(t) = 0$である時間の関数$f(t)$は$\int_{-\infty}^{\infty}|f(t)|dt < \infty$を満たすとする．このような関数$f(t)$のラプラス変換は下記で与えられる．
$F(s) = \int_{0}^{\infty}f(t)e^{-st}dt \ \ \ \ \ $(1-1)

ここで$s$はラプラス変数で複素数$s = \sigma + j\omega$である．ただし$\sigma$は導電率の意味ではなく，複素数の実数項を意味するのみである．$j$は単位虚数で$j^{2} = -1$である．$\omega$はオイラーの公式から周期性に関わる変数になるため角周波数になる．

式(1)は時間（$t$)の関数を複素数（$s$）の関数への写像変換である．表記を簡素化するためラプラス変換を下記で表記する．
$F(s) = \mathcal{L}[f(t)] \ \ \ \ \ $(1-2)

合成関数の微積分を組み合わせると下記関係を導出することができる．
$\mathcal{L}[\frac{df(t)}{dt}] = sF(s) - f(0)\ \ \ \ \ $(1-3)

$\mathcal{L}[\int f(t)dt] = \frac{F(s)}{s}\ \ \ \ \ $(1-4)

$f(0)$は初期値である．インピーダンスなどの信号応答測定では初期値依存性がないため式(1-3)の$f(0)$は0になる．式(3)と(4)から時間領域の関係が線形微積分関係で与えられるものに対してラプラス変換を施すと微積分演算子がとれ簡単な四則演算式に変わることがわかる．ラプラス変換によって写像された領域をラプラス領域と呼ぶ．

ラプラス変数$s$を$j\omega$に変換・写像するのがヘヴィサイド変換である．ラプラス変換後，ヘヴィサイド変換を行うとフーリエ変換と等価な関係に変わる．したがってヘヴィサイド変換はラプラス領域の関数をフーリエ領域の関数に写像する変換である．時間領域関数をフーリエ変換で写像しないのは式(1)に相当するフーリエ変換式が収束しない，または0になる場合があり，インピーダンスの定義式が当てはまらないケースがあり得るためである．電気化学インピーダンス解析の場合，$f(t)$, $F(s)$の具体解を求める必要はない．したがって写像変換によって電流と電圧を表す関数が，異なる変数を持つ電流と電圧の関数に変換されることのみ理解すればよい．

時間領域における電流[$i(t)$]と電圧[$v(t)$]の関係をラプラス変換，ヘヴィサイド変換によりフーリエ領域に写像し，オームの法則と同様に電流[$I(j\omega)$]を電圧[$V(j\omega)$]で割った関数がインピーダンス[$Z(j\omega)$]となる．変換関係を理解できればインピーダンスは$\omega$の関数ではなく$j\omega$の関数であることも理解できるだろう．

インピ－ダンスの説明で「交流場では電圧と電流は$e^{j\omega t}$に比例するので・・・」とする説明をよく見かける．この方法は上記の変換を簡便に行う代替法だ．ただし写像変換という重要な基礎を述べていないことは問題だろう．このような説明では，どの領域の話を進めているのか曖昧になるためだ．「実時間では$V_{0}e^{j\omega t}$の実数項電圧が印加され，$I_{0}e^{j\omega t}$の実数項電流が流れている（が，交流を表すためには実世界に存在せず測定もできない虚数項を組み込んだ式を使って良い）」「交流電圧は$V_{0}e^{j\omega t}$とすると数学的な取り扱いが一般化できる」などは意味不明だ．信号解析のみ奇妙な解釈が許される，というのは変だと感じるのが自然だろう．さらに大きな問題は，曖昧な解釈では経験則パラメータが何を表しているか？を考える道筋さえも見失ってしまうことだ．

ページトップに戻る

2．実例（コンデンサーのインピーダンス）

コンデンサーの容量($C$)が微分形式で与えられるとする．蓄電された電荷量($Q$)と電圧($v$)の関係は下記で与えられる．
$C = \frac{dQ}{dv} \ \ \ \ \ $(2-1)

電荷量($Q$)と電圧($v$)が時間変動するとする．式(2-1)の両辺を時間で微分すると下記関係を得られる．
$\frac{dQ(t)}{dt} ≡ i(t) = C\frac{dv(t)}{dt}\ \ \ \ \ $(2-2)

式（2-2)に(1-3)とヘヴィサイド変換を適用すると，
$I(j\omega) = Cj\omega V(j\omega)\ \ \ \ \ $(2-3)

となる．インピーダンス[$Z(j\omega)$]は，電圧[$V(j\omega)$]を電流[$I(j\omega)$]で割ったものであるから,
$Z(j\omega) = \frac{V(j\omega)}{I(j\omega)}= \frac{1}{Cj\omega}\ \ \ \ \ $(2-4)

を導出できる．時間領域式(2-2)では容易に求められない$v/i$の関係がラプラス領域，フーリエ領域であれば容易に求められることが解るだろう．

逆に現実に合わせて印加電圧$v(t) = v_{0}\rm {sin}(\omega t)$とすると式(2-3)さえ求められない．これは時間領域から出られないためだ．さらに$Z = v(t)/i(t)$としてしまうと周期的な発散が生じることも気付くだろう．インピーダンスの理解には写像による領域変換を理解することが必要不可欠なのだ．

ページトップに戻る

3．経験則パラメータの意味（デバイの経験則スペクトルを例に）

フーリエ領域におけるデバイの経験則スペクトル(R//CPE)の関係を時間領域の関係に逆変換してみよう．なぜなら通常の説明である「容量」や「円弧の潰れを表すパラメータ」の真の意味がわかるからだ．

デバイの経験則スペクトル式（R//CPE）は下記で与えられる．
$Z(j\omega) = \frac{V(j\omega)}{I(j\omega)} = \frac{R}{1+RT(j\omega)^{\alpha}}\ \ \ \ \ $(3-1)

ここで$R$は抵抗，$T$はConstant Phase Element（CPE）の疑似容量，$\alpha$は円弧のつぶれを与えるパラメータ，フラクタルパラメータ等と呼ばれる．式(3-1)の逆数にして変形すると下記を求められる．
$I(j\omega) = \frac{V(j\omega)}{R} + T(j\omega)^{\alpha}V(j\omega)\ \ \ \ \ $(3-2)

式(1-3)で式(3-2)を逆算することはできない．なぜなら$(j\omega)^{\alpha}$項を説明できないからだ．式(1-3)とヘヴィサイド変換で$j\omega$項が現れるのは時間に対する１階微分によることに注目する．同じ規則が存在するならば$(j\omega)^{\alpha}$は時間に対する$\alpha$階微分によると予測される．非整数階の微積分は分数階微積分と呼ばれる数学領域に存在する（教科書１，教科書２）．この数学を参考にすると式(3-2)は下記時間領域式に変換できる．
$i(t) = \frac{v(t)}{R}+ T\frac{d^{\alpha}v(t)}{dt^{\alpha}}\ \ \ \ \ $(3-3)

ここで$\frac{d^{\alpha}}{dt^{\alpha}}$は時間に対する分数階微分演算子を示す．CPEの$T$パラメータは電圧の時間に対する$\alpha$階微分係数，$\alpha$は微分階数であることがわかる．R//CPEモデルのインピーダンス解析では微分階数をパラメータにしていたのだ．さらにTの単位は$\alpha$に依存する．$\alpha = 1$の時のみ$T$の単位から$\alpha$が消える関係にある．

分数階微分は整数階微積分を補完するよう組み立てられた数学である．実描像があるのは整数階微積分のみであり，分数階微積分そのものの実描像はわかっていない．したがって式(3-3)自体の物理描像はないに等しい．これを考慮しながら式(3-3)を見直すと下記が結論として導かれる．

• デバイの経験則スペクトル式そのものに明確な物理描像はない
• デバイの経験則スペクトル式の抵抗に定義の変更はない
• CPEの疑似容量は容量とは全く異なる定義係数である
• デバイの経験則スペクトル式で分離された抵抗に物理的意味があるとは限らない

本来CPEや経験則パラメータは安直に導入すべきものではない．スペクトル形状の観察のみから等価回路モデルを推定しなくてはならない状況で必要悪として用いるのだ．Warburgインピーダンス，Gerischerインピーダンスの経験則パラメータを変数あるいは理想値と異なる値にすることはフィックの拡散法則，特に第２法則を否定していることを意味する．経験則パラメータを用いるならば，本当は既存の物理法則を否定する覚悟とそれを説明する責任を伴わなければならない．

非理想的な形状のスペクトルを経験則パラメータを導入することなく解くことができるソフトウェアも存在する．

K. Kobayashi, Y. Sakka, "Development of an electrochemical impedance analysis program based on the expanded measurement model", J. Ceram. Soc. Jpn., 124 (2016) 943-949.DOI: 10.2109/jcersj2.16120

K. Kobayashi, T. S. Suzuki, "Development of an Algorithm for Automatic Analysis of the Impedance Spectrum Based on a Measurement Model", J. Phys. Soc. Jpn., 87 (2018) 034004.DOI: 10.7566/JPSJ.87.034004

しかしその解析法は主流になっていない．

ページトップに戻る

4．複素非線形最小二乗法

現代ではインピーダンスを複素数で表記する．インピーダンス・スペクトル・モデル解析においては，複素関数モデルに対してパラメータを実数に拘束して最小自乗を実行する．複素非線形最小自乗計算は現代の汎用非線形最小自乗モジュールで対応することができる（例えばScilabやR）．具体的なプログラムの書き方は言語に依存するため，ここでは概要のみを記す．

1. パラメータ配列と周波数を入力すると複素数形式インピーダンス値を返す関数を定義
2. 入力周波数配列サイズを確認し，配列サイズの1/2より上位項の周波数に対してはインピーダンス実数項を，1/2以下の周波数にたいしてはインピーダンス虚数項を返す関数を定義
3. 測定周波数を２つ結合した配列を作成
4. インピーダンス実数項と虚数項を結合した配列を作成
5. 関数(2)と配列(3), (4)を用いて非線形最小自乗法を実行

これだけで複素非線形最小自乗法を実装できる．複素関数を計算機内部で実数関数化して最小自乗法を適用しているのだ．非線形最小自乗モジュールには自乗残差和を最小にするパラメータを繰り返し計算で探索するアルゴリズムが実装されている．pyZwxではLmfitの拘束付きLevenberg-Marquardt法を使用している．

上記表記の場合複素非線形最小自乗法で最小化する自乗残差和($S$)は下記で与えられる．
$S = \sum_{k=0}^{k=l-1}\frac{\left(Z^{data}[k]-Z^{model}_{real}[k]\right)^2}{w[k]} + \sum_{k=l}^{k=2l-1}\frac{\left(Z^{data}[k]-Z^{model}_{imag}[k]\right)^2}{w[k]}\ \ \ \ \ (4-1)$

$l$は実測定データ数，$Z^{model}[k]$は上記(4)で作成したインピーダンス・データ配列の$k$番目項，$Re()$, $Imag()$はインピーダンス実数項および虚数項を抽出する関数，$Z^{model}[k]$は(3)で作成した周波数配列の$k$番目項から計算されるインピーダンスモデル値，$w[k]$は$k$番目インピーダンスの重み係数である．理想的な重み係数は各データの標準偏差である．重み係数については次項に記す．

ページトップに戻る

5．pyZwxで実装した重み付け

通常インピーダンス測定データには各データ点における標準偏差は含まれていない．したがって式(4-1)の重み係数$w[k]$は標準偏差に比例する値を代替で用い，標準誤差計算時に規格化を行う．インピーダンス解析では$w[k] = |Z[k]| = \sqrt{Z^{2}_{real}[k] + Z^{2}_{imag}[k]}$を用いているソフトウェアが多い．$Z_{real}[k]$，$Z_{imag}[k]$は周波数配列の$k$番目周波数におけるインピーダンス実数項と虚数項を示す．$Z_{real}[k]$，$Z_{imag}[k]$には測定データを用いるもの，計算モデル値を用いるものがある．pyZwxではWeight Typeで|Zm|を選択すれば測定データ値，|Zcal|を選択すればモデル値が使用される．

pyZwxではさらに一般化を進め，$w[k] = \left(Z^2_{real}[k] + Z^2_{imag}[k]\right)^{pf/4}$の形式で設定できるようにしている．$pf$は指数係数（Power Factor）である．指数係数を変えられるようにしたのはデータや非線形最適化法に依存して最適な指数係数が異なる傾向があったためである．

ここで$w[k] = |Z[k]| = \sqrt{Z^2_{real}[k] + Z^2_{imag}[k]}$であるとき，暗黙に導入される仮定に注目しよう．この設定では，ある周波数で測定されるインピーダンス実数項と虚数項が等しい標準偏差を持つと仮定される．もし実数項と虚数項が異なる標準偏差を伴っている時にはインピーダンス実数項と虚数項の重み係数は異なる値を用いなければならない．この設定に該当するのが|Zm_r| & |Zm_i|および|Zcal_r| & |Zcal_i|である．この設定ではインピーダンス実数項および虚数項の標準偏差がそれぞれの値に比例していると仮定される．この仮定はもっともらしく思えるが非常に発散しやすく実用的ではない．

重み付けを使わない設定がUnit Weightで，$w[k] = 1$とするものである．この重み付けではインピーダンス実数項と虚数項がすべて等しい標準偏差を伴っていると仮定されている．この重み付けは測定周波数範囲でインピーダンス値の桁数がほぼ変わらないようなデータであれば使用できる．しかしインピーダンス値の桁が小さい領域におけるモデルへの適合化が弱くなる．

$w[k] = |Z[k]| = \sqrt{Z^{2}_{real}[k] + Z^{2}_{imag}[k]}$の重み付け設定は広い周波数領域，広い$|Z|$領域で最適化ができる一方で，データの標準偏差について少々疑問が残る設定であることは頭の片隅に置いておくべきだろう．

各測定データにおける標準誤差を出力する装置があればデータの重み付け問題は解決される．その代わりソフトウェアの改訂が要求されるだろう．

ページトップに戻る

6．等価回路

電気化学インピーダンスの教科書において，等価回路の説明は抵抗と容量の直列接続と並列接続から始まるものが多い．この説明では直並列接続時のインピ－ダンス値の計算法が記載されている．インピーダンスという摩訶不思議な量の計算法を説明するがごとくだ．ここでは少し異なる説明をしよう．

電流，電圧，時間の関係が異なる２つの素子，抵抗（$R$）とコンデンサー（$C$）からなる回路の時間変動関係を考えよう．この場合，２種類の回路が想定できる．すなわち２つの素子に(1)同一の電圧が印加されながら異なる電流が流れる回路，(2)同一の電流が流れながら異なる電圧が印加される回路である．

抵抗の電流($i(t)$と電圧（$v(t)$）の間には$v(t) = Ri(t)$（オームの法則）が成り立つ．コンデンサーには式(2-2)が成り立つ．

上記(1)の場合，$i(t)$は下記で与えられる．

$i(t) = \frac{v(t)}{R} + C\frac{dv(t)}{dt}\ \ \ \ \ $(6-1)

式(6-1)にラプラス変換とヘヴィサイド変換を施すと，下記式が導き出される．

$I(j\omega) = \frac{V(j\omega)}{R} + Cj\omega V(j\omega)\ \ \ \ \ $(6-2)

インピーダンスの定義から

$Z(j\omega) = \frac{V(j\omega)}{I(j\omega)} = \frac{R}{1+RCj\omega}\ \ \ \ \ $(6-3)

この関係は$R$と$C$の並列接続回路のインピーダンス式である．並列回路とは複数の素子に同一の電圧が印加される回路なのだ．

上記(2)の場合を考えよう．式(2-2)を時間で積分し，かつ$v(t = 0) = 0$とすると，コンデンサーに対して下記式が導出できる．

$v(t) = \frac{1}{C}\int_0^t i(t) dt\ \ \ \ \ $(6-3)

オームの法則と(6-3)式を組み合わせると，下記関係が導出できる．

$v(t) = Ri(t) + \frac{1}{C}\int_0^t i(t)dt\ \ \ \ \ $(6-4)

(6-4)式にラプラス変換とヘヴィサイド変換を施すと，

$V(j\omega) = RI(j\omega) + \frac{I(j\omega)}{Cj\omega}\ \ \ \ \ $(6-5)

インピーダンス定義式から下記関係を導出できる．

$Z(j\omega) = \frac{V(j\omega)}{I(j\omega)} = R + \frac{1}{Cj\omega}\ \ \ \ \ $(6-6)

これは直列接続式である．直列接続とは複数素子に同一電流が流れる回路であることがわかる．

インピーダンスは摩訶不思議な量ではなく，電圧，電流，時間の関係から導出できる量だ．これに位置の情報が関わる場合にWarburgインピーダンス，Gerischerインピーダンスが導出される．ただしインピーダンスに変換される情報は電流，電圧と時間であるため位置の情報は間接的なものとなる．たとえば全固体系の場合，位置は固体電解質と電極の界面に固定されるのである（文献）．複雑な伝送線モデルを考察する間に基本的なことを忘れてしまったらしい論文は数多く出版されている．

ページトップに戻る

7. インピーダンスのデータ構造とグラフ表示

インピーダンスはフーリエ領域で定義される量なので複素数で表記される（参照：1. インピーダンスの基礎）複素数表記のインピーダンスを$\bf Z$と表記する．$\bf Z$に対する可変量は周波数（あるいは角周波数）である．したがって周波数は$\bf Z$に対して直交する．$\bf Z$の実数項と虚数項を$Z_{\rm real}$, $Z_{\rm imag}$とすると$Z_{\rm real}$と$Z_{\rm imag}$の間にも直交関係がある．これらをまとめると周波数-$Z_{\rm real}$-$Z_{\rm imag}$の軸は直交した3次元空間を作ることがわかる．インピーダンスはこの3次元空間内の数値集合である．

この3次元空間における$\bf Z$に適合するモデルを与えるのが等価回路推定である．3次元構造を表示されたグラフから正しく読み取ることは難しい．したがってモデル構築をサポートする適切なグラフ表示が必要不可欠になる．2次元面に描かれた3次元グラフは読み取りが難しいため2つの直交軸からなる平面への投影曲線を使う．インピーダンスの場合，慣例でインピーダンス・プロット（$Z_{\rm real}$-$Z_{\rm imag}$プロット）のみを使用させるように表示するソフトウェアが多い．しかしデータ構造を考えるとインピーダンス・プロットのみでは情報劣化が生じる．なぜなら周波数情報がグラフから消えているからだ．したがってインピーダンスをグラフで正確に表示するにはインピーダンス・プロットに加え，$\rm log (\it f \rm) - \it Z_{\rm real}$プロットと$\rm log (\it f \rm) - \it Z_{\rm imag}$プロットを並列表示するべきなのだ．またインピーダンス測定の場合，系によっては$|\bf Z \rm |$値が桁で変化することも多い．このような場合，$Z_{\rm real}$，$Z_{\rm imag}$よりも$\rm log |\it Z_{\rm real}\rm |$，$\rm log |\it Z_{\rm imag}\rm |$でプロットした方がスペクトル構造の詳細を見やすい．

インピーダンスのデータ構造を理解できればインピーダンス・スペクトルデータの表示に，インピーダンス・プロットとボード線図（対数周波数とインピーダンス絶対値（$|Z|$）および対数周波数と位相角（$\phi$）のプロット）を並列表示するのは賢明でないこともわかるだろう．周波数-$Z_{\rm real}$-$Z_{\rm imag}$からなる3次元空間情報の一部を極座標変換して，周波数-$Z_{\rm real}$-$Z_{\rm imag}$に$|Z|$-$\phi$という2つの量を水増ししてしまうからだ．$|Z|$-$\phi$は$Z_{\rm real}$-$Z_{\rm imag}$に変換可能なのだから無意味に表示量を増やす必然性は無い．

インピーダンス・プロットではスペクトルの形状から等価回路を推定する．したがってインピーダンス・プロットを作製するときには$Z_{\rm real}$と$Z_{\rm imag}$軸の単位長さを等しくして描画しなくてはならない．pyZwxで用いたMatplotlibには自動で軸の単位長さをそろえてくれるスイッチが実装されている．pyZwxではメインウィンドウのサイズをユーザーが任意に変えてもインピーダンス・プロットの単位軸長さは等しくなるよう自動で設定される．同様のプロット機能はGnu plotの他，MatLab, Scilab, R等のプロット関数にも実装されている．

具体例を示す．pyZwxのデモデータに対して，下記モデルと初期値を入力してスペクトルを計算する．
R0 + R1//CPE1 + R2//CPE2 + R3//CPE3
R0: 12
R1: 2
CPE1_T: 1e-5
CPE1_a: 0.8
R2: 6
CPE2_T: 1e-3
CPE2_a: 0.6
R3: 4
CPE3_T: 1e-2
CPE3_a: 0.7
インピーダンス・プロットは下記になる．一見，初期値としては問題がない値のように見える．

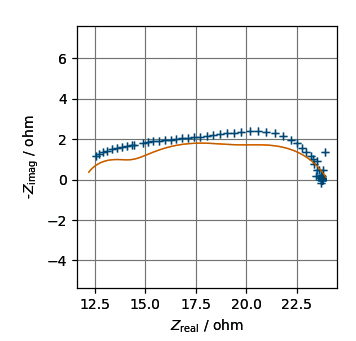
しかし$\rm log \it f - Z_{\rm imag}$プロットを見ると推定スペクトルは実測値とまったくあっていない．特にピーク周波数のずれが大きいことがわかるだろう．

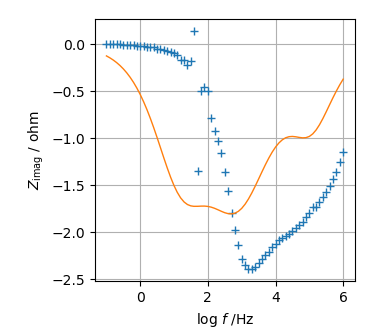
このような解から大きく外れた初期値から複素非線形最小自乗計算を実行すると最悪の場合，計算は発散する．モデルとパラメータ初期値の可否を見るのにインピーダンス・プロットのみでは不十分とわかるだろう．

別の例を見てみよう．下のインピーダンス・プロットは標準セル（SolarTron12961）を用いて測定したものである．

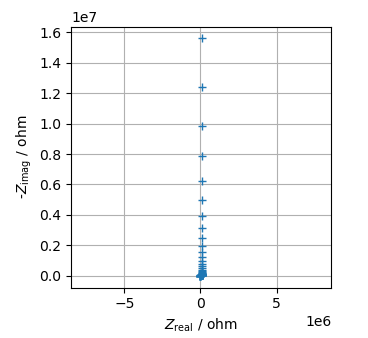
一見，単純な抵抗と容量の直列回路スペクトルに見える．しかし$\rm log (\it f \rm) - log |\it Z_{\rm imag}\rm |$プロットの$\rm log \it f \rm $ = 3~4の領域でS状曲線を描いていること，$\rm log (\it f \rm) - log |\it Z_{\rm real}\rm |$プロットの高周波数限が一定値に収束していないことから，当てはめるべき等価回路はR0 + C0ではないことがわかる．
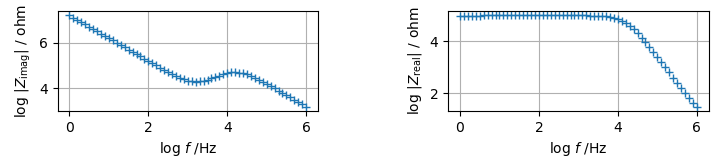
このスペクトルに対する回路の正解はC0//(R1+C1)である．先見情報を持たない場合，このスペクトルをR0//C0 + C1と推定するのは仕方ないことだろう．実際，C0//R0 + C1モデルでも最適化可能だ．

最適化したモデルと実測値が合っているかは測定データマークと計算曲線が一致しているかによって判定する．この判定に用いる情報は両者の差分をとることで抽出できる量だ．モデルが悪い場合，残差曲線がホワイトノイズ状にならず連続的な曲線になる．したがって残差曲線をみるとモデルの善し悪しを判定できる．

pyZwxではデータを読み込むと6つのグラフが一つのウィンドウに表示される．これは見栄えのためでは無く上記のデータ構造と機能を考えてデザインした結果なのだ．

ページトップに戻る

8. インピーダンスと複素誘電率

フーリエ領域で定義される電気的特性量はインピーダンスの他，アドミタンス（admittance），誘電率（permittivity），電気的モジュラス（modulus）がある．測定装置のソフトウェアによっては，これらの量が相互変換できるようになっている．一つの測定で複数の電気的特性量が求められる関係がどのようになっているのか？説明を探すのは難しい．なぜなら変換関係の表を記載する文献は見つけやすい一方で，その変換関係がどのように導出できるかを記載した文献や教科書が少ないからだ．ここではインピーダンスと電流の定義式を組み合わせた式から，これらの関係を見直そう．

インピーダンスの定義式は式(2-4)にもあるように下記で与えられる．

$Z(j\omega) = \frac{V(j\omega)}{I(j\omega)}\ \ \ \ \ $ (8-1)

$I(j\omega) = j\omega Q(j\omega)\ \ \ \ \ $ (8-2)

(8-2)は式(2-2)から求められる．

アドミタンス[$Y(j\omega)$]はインピーダンスの逆数なので

$Y(j\omega) = \frac{1}{Z(j\omega)} = \frac{I(j\omega)}{V(j\omega)}\ \ \ \ \ $ (8-3)

式(8-3)最右辺関係に式(8-2)を代入すると

$Y(j\omega) = \frac{j\omega Q(j\omega)}{V(j\omega)} = j\omega C_{0}\epsilon^{*}(j\omega)\ \ \ \ \ $ (8-4)

ここで複素誘電率[$\epsilon^{*}(j\omega)$）]は空セル容量（$C_{0}$）を用いて下記で与えられるからだ．

$\frac{Q(j\omega)}{V(j \omega)} = C_{0}\epsilon^{*}(j\omega)\ \ \ \ \ $ (8-5)

式(8-4)の逆数から電気的モジュラス[$M~{*}(j\omega)$]が求められる．

$M^{*}(j\omega) = \frac{1}{\epsilon^{*}(j\omega)} = \frac{j\omega C_{0}}{Y(j\omega)}\ \ \ \ \ $ (8-6)

(8-6)と(8-3)を組み合わせると下記関係が求められる．

$M^{*}(j\omega) =　j\omega C_{0}Z(j\omega)\ \ \ \ \ $ (8-7)

これらの関係は基点にする式によらず同一の相互関係を求めることができる．さらにインピーダンスとアドミタンスの可測量は電流と電圧でとっているのに対し，複素誘電率と電気的モジュラスの可測量は電荷量と電圧になっていることがわかる．これらの関係が変換可能なのは式(2-2)で示した様に電荷量の時間変動が電流になるという関係によるのだ．何らかの物理現象をインピーダンス・スペクトルから議論する時，インピーダンスと複素誘電現象を別々のものの様に扱う論文を見かけることがある．そのような取り扱いは誤解を招きやすいこともわかるだろう．

ページトップに戻る