 |
A femtosecond laser pulse can initiate collective, in-phase atomic motions in solids called coherent phonons. Here’s a simple explanation on how they are created and eventually come to the end of their lifetime. |
Atoms in materials are always in motion. In solid materials they can move collectively, and their motions are called phonons (as quasi-particles in quantum mechanics).
Solids typically contains huge number of atoms, which usually move indifferently to each other -- or at random phase. When the atoms receive impulsive force from outside, however, they can start to keep pace with their neighbors -- or become in-phase. These atomic motions are called coherent phonons.
Like phonons in general, coherent phonons are also categorized into acoustic and optical branches. Coherent optical phonons are standing waves of in-phase atomic vibrations over macroscopic spatial range. Coherent acoustic phonons are strain or shear wavepackets propagating ballistically in solids.
Our lab studies both coherent optical and acoustic phonons experimentally to reveal the electron-phonon coupling dynamics in the target material.
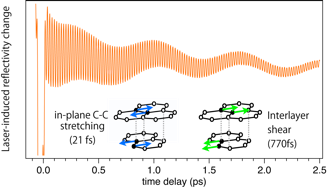
Coherent optical phonons of graphite:
Pump-induced periodic atomic vibrations modulate reflected probe intensity in the real time in pump-probe scheme. Fast and slow oscillations are due to in-plane C-C stretching and interlayer shear with periods of 21 and 770 femtoseconds. The periods are characteristic of materials but independent of probe wavelength. |
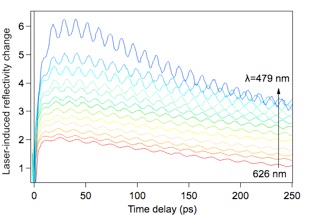
Coherent acoustic phonons of CaP:
Propagation of pump-induced strain pulse in crystal modulates reflected probe intensity in pump-probe scheme by acting like a moving mirror in one arm of an interferometer (aka Brillouin oscillation). Period of the modulation, typically tens of picoseconds, depends on the wavelength λ of the probe light. |
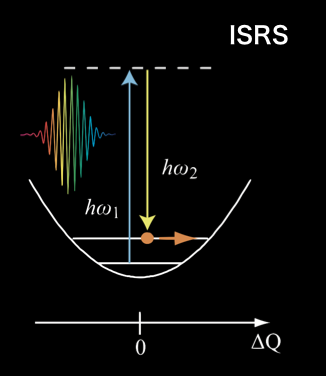
How can a femtosecond laser pulse induce coherent phonons in solids? The answer depends on the solid as well as the phonon mode.
When solid is transparent to incident light pulse, or when photoexcitation is non-resonant, coherent optical phonons are generated exclusively via impulsive stimulated Raman scattering (ISRS) [1].
- A femtosecond laser pulse has a broadband spectrum, broad enough to contain many pairs of photons whose energies are different by the phonon energy.
The resulting oscillation is a sine function of time (zero amplitude at time zero). The amplitude of the induced oscillation can depend on the polarization of the incident light according to the Raman selection rule.
When solid is opaque, or when photoexcitaiton is resonant, the situation can be more complicated.
-
Resonant ISRS can always contribute to the coherent phonon generation in such a condition (phonon mode symmetry, laser wavelength and polarization, etc.) as spontaneous resonant Raman scattering takes place [2].
-
The resonant behavior (as a function of excitation wavelength) should follow that of the spontaneous Raman scattering. The initial phase can deviate from a sine function of time, depending on the duration of the driving force [3].
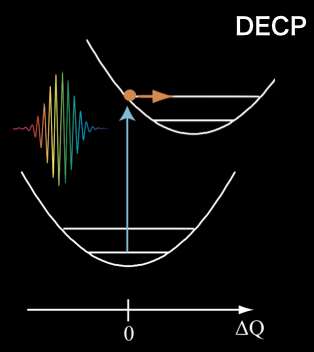
In addition, non-Raman excitation mechanisms have also been proposed for particular types of materials and phonon modes.
-
For solids with Peierls distortion, such as Bi and Sb, a generation mechanims called displacive excitation of coherent phonons (DECP) was proposed [3].
- In this model, sudden creation of photoexcited carriers shifts the vibrational potential minimum for the A1g mode, which is associated with the Peierls distortion. The initial phase of the coherent phonons in this case depends on the decay time of the photoexcited carriers [3]. When the decay time is much longer than the phonon period, it approaches a cosine function time.
- For the E1g mode of the same semimetals, which are not directly associated with the Peierls distorsion, coherent phonons are excited via ISRS [4].
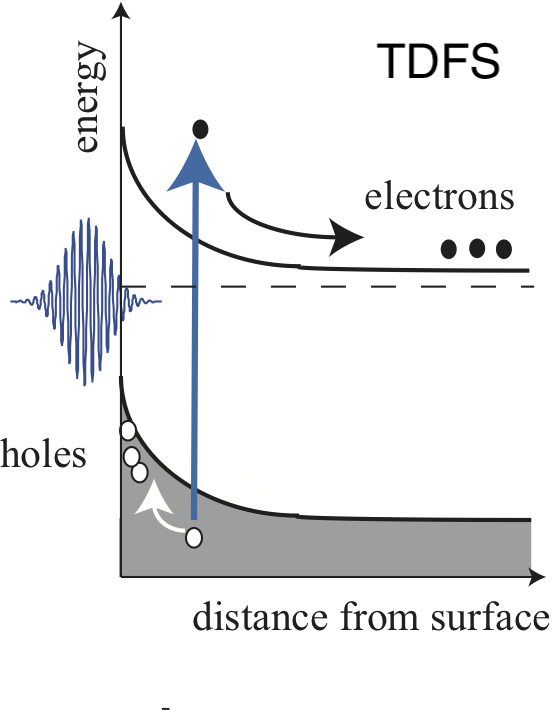
- For a surface depletion layer of polar semicomductors, transient depletion field screening (TDFS) model, in which photoexcited carriers suddenly screen the depletion field, has been proposed [5]
- In this mode, electron and hole plasmas photoexcited in the depletion region drift in the opposite directions and thereby screen the depletion field. This sudden change of the electric field triggers in-phase motion of positive and negative ions. The TDFS model is particularly relevant for the longitudinal optical phonons of GaAs and other III-V semiconductors. In the depletion region, Whereas the GaAs LO phonons can be generated via both resonant ISRS and TDFS, their contributions can be distinguished experimentally based on their different polarization-dependences [6,7].
Coherent acoustic phonons are generated by a single laser pulse under resonant excitation condition. The following three generation mechanisms have been proposed.
- Thermoelastic effect [8]
- Laser heating induces sudden expansion of the crystalline lattice, mainly in metals.
- Deformation potential coupling [8]
- Photoexcitation modifies electronic energies at different points in the Brillouine zone and thereby causes atomic displacements, mainly in semiconductors.
- Piezoelectric screening [9]
- Photoexcited carriers screen the built-in piezoelectric field, for example at (111)-oriented polar semiconductor surfaces and interfaces.
Phonons, either incoherent or coherent, do not live long. Acoustic phonons can live up to microseconds at low temperatures, but optical phonons have less-than-a-nanosecond lifetime.
In a perfect crystal, anharmonic coupling between normal modes provides the main path for the decay of phonons. The simplest case is the spontaneous decay of an phonon into two phonons of lower frequency . Temperature dependence of the decay rate (or linewidth) can reveal this anharmonic process [10].
Scattering by crystalline defects such as impurity atoms, atoms with different isotopic masses and vacancies can annihilate phonons effectively [11].
Electron-phonon coupling can dominate the decay of phonons in metals and semimetals in the presence of carriers at high density, e.g. under intense photo-excitation or application of external electric field [12]. In low-dimensional systems such as graphite and carbon nanotubes, high-frequency optical phonons can decay by creating electron-hole pair near the Fermi level. In such cases, photoexcitation can prolong, instead of shorten, the lifetime of the optical phonons [13].
- References
- Dhar et al. Chem. Rev. 94, 157 (1994).
- Stevens et al, Phys. Rev. B 65, 144304 (2002).
- Zeiger et al., Phys. Rev. B 45, 768 (1992).
- Ishioka et al. J. Appl. Phys. 100, 093501 (2006).
- Pfeifer et al., Appl. Phys. A 55, 482 (1992).
- Yee et al., Phys. Rev. Lett. 86, 1630 (2001).
- Ishioka et al., Phys. Rev. B 84, 235202 (2011).
- Thomsen et al., Phys. Rev. B 34, 4129 (1986).
- Sun et al., Phys. Rev. Lett. 84, 179 (2000).
- Hase et al. Phys. Rev. B 58, 5448 (1998).
- Ishioka et al. Physica B, 316-317, 296 (2002); Appl. Phys. Lett. 78, 3965 (2001).
- Misochko et al., J. Phys.: Cond. Mater. 19, 156227 (2007).
- Ishioka et al., Phys. Rev. B 77, 121402R (2008).






