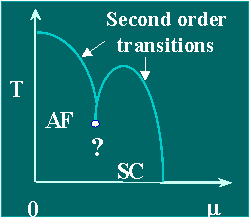
Fig.1: schematic picture of the phase diagram of high-Tc superconductor
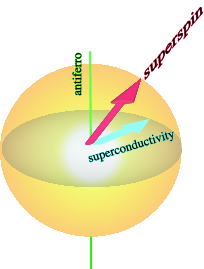
Fig2: picture of 5-component superspin

Fig.3
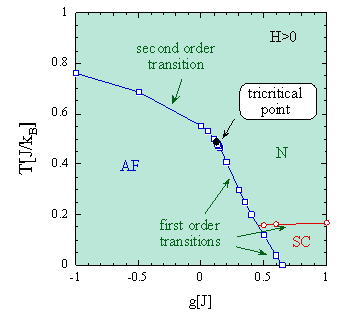
Fig.4
Extending our previous methods and experience to simulate the 2-component
order parameter of the superconductor (i.e. the XY model) to the 5-component
superspin, we have conducted extensive numerical studies of a lattice version
of the SO(5) theory. We believe our results are noteworthy; phase diagrams
for part of our work are displayed. Our results should also be relevant
to the phase diagrams of organic superconductors where similar behavior
has been observed.
Recent work has focused on the bicritical phenomenna between the AF and
SC phases, a hallmark of the SO(5) theory(Fig.3).Besides successfully computing
the critical exponent upon the approach to the bicritical point (which
will let experiments decide whether they are indeed observing the trace
of the "number 5" of the theory), we have demonstrated that the
bicritical point is stable with respect to repusive AF-SC fluctuations,
contrary to the epsilon-expansion results.
Figure 4 depicts the phase diagram for the case with an applied magnetic
field. We find a tricitical point on the Neel transition line ( N(normal)
to AF ) at which the transition switches from first to second order. The
effect of superconducting fluctuations is responsible for the change to
the first order transition, an important implication of the SO(5) theory.