
グループ研究に戻る>
To English contents>
広義の透過電子顕微鏡法は、結像法・回折法・分光法を含み、様々な計測が可能です。これまで、電子顕微鏡グループで行ってきた研究を中心に、透過電子顕微鏡法の研究と材料評価の内容を、計測手法毎に紹介します。
球面収差補正装置が実用化される前、高分解能透過電子顕微鏡法は、電子の波長が短い超高圧電子顕微鏡を用いて行われていました。我々は超高圧電子顕微鏡(加速電圧1MeV)を用いて、単結晶MgO中に埋め込まれたAu微粒子を観察しました。MgOの格子縞が観察の妨げにならないように、結晶軸から試料を意図的に傾斜するoff-Bragg条件にして、Au数原子からなるクラスターのみを結像しました(電子顕微鏡学会論文賞(第6回1991)。美浜先生田中信夫先生のご指導によるものです)[JEM 1989]。超高圧電子顕微鏡の操作方法は荒井重勇先生に厳しく指導を受けました。

コマ収差はTEM像の分解能を制限するため計測して補正する必要があります。しかしコマ(2次幾何収差)は非点収差とは異なり、TEM像をフーリエ変換しただけでは測れません。我々は1枚の画像からコマフリー軸調整する方法を提案しました[Ultramicroscopy 2003]。 提案した手法では、試料による回折・散乱を、振幅分割型のビームスプリッターとして使い、球面収差などによる火面(Caustic figure)を利用します。結晶性試料を用いれば球面収差や焦点はずれ量を計測することも可能です。

スルーフォーカス(焦点を連続変化させた)TEM像を3次元フーリエ変換することにより、空間分解能(情報限界)を定量的に求める方法を提案しました。現在も用いられているYoung's fringe法では、非線形結像成分のため情報限界を正確には評価できません。基本原理は1990年代に生田・志水・高井・谷口ら(敬称略)が提案した「能動型画像処理」に基づいています。NIMS自作のDigitalMicrograph用Scriptを用いて、スルーフォーカス像計測やドリフト補正あるいは3Dフーリエ変換などを行い、低加速電子顕微鏡やモノクロメーターTEMの空間分解能を求めました [Ultramicroscopy 2012], [2013]。 JST-CREST Triple-C project(代表末永先生)に参画させていただき、日本電子の沢田さん佐々木さんと協力し、低加速TEM像の分解能評価なども行いました。
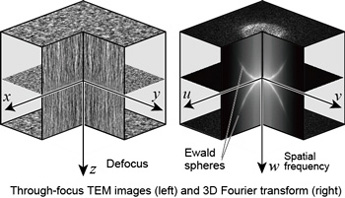
球面収差補正TEMによる高分解能観察を、NIMSの佐々木高義フェローが合成したTiO2ナノシートの観察に適用しました。電子照射により形状を保ったままTi2O3シートに還元されることや[JCPL 2011]、Ti点欠陥の直接観察を行いました[Sci.Rep.2013]。
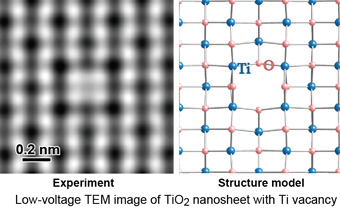
これまで電子顕微鏡用のカメラをいろいろと使ってきましたが(SlowScan CCD, MultiScan CCD, UltraScan CCD, OneView, RIO, K2)、カメラの感度係数(conversion efficiency)は装置や加速電圧によって変化します。我々の実験装置には、加速電圧の値から感度計数を書き換えるscriptが入れてあり、カメラの信号強度は常に電子の数に変換しています。 科研費(20H02624)の成果で、さらにその値を使ってプローブ電流もサブピコアンペアまで計測可能です。
電界放出型TEMにGatan社のEnergy filterを組み合わせ、金属多層膜を1nmの分解能でマッピングをしました[JJAP1994], [1995]。半導体用絶縁材料(SiO2やSi3N4あるいは層間絶縁膜)の観察にも適用しました[応用物理学会奨励賞(1997)]]。その後、共同研究者からの要求に基づき、当時まだ定性的だった元素マップを初めて定量的に観察しました。磁気記録媒体CoCrの観察では磁気特性と基板温度の相関を元素マップから明らかにしました[JJAP 1995]。 CrとCoの組成比が定量できればスレーターポーリング曲線から磁気特性がわかるからです。ステンレス鋼では、鋭敏化処理によるCr欠乏層の観察を行いました[JEM 1996] 。ステンレス鋼ではCr組成が10%程度以下になると耐食性が低下するため、Cr組成の定量値が重要です。

電子分光器の焦点を調整して、複数位置のスペクトルを同時に計測できる手法を位置分解EELSと名付けました[JEM 1997]。この手法は1960年代に渡辺宏(日立)さんがメーレンシュテット分光器で行っていた角度分解EELSを実空間にしたものです。SiのL殻やK殻のケミカルシフトを正確に計測したほか、半導体用プロセスで製膜したSiO2/SiN/SiON/Si基板のケミカルシフトを計測しました[Microscopy 2001]。
その後半導体MIRAIプロジェクトに参画し、位置分解EELSを用いて、Al2O3/Si界面のAlの配位数変化を解析しました[APL 2003]。 溝口先生・田中功先生による第一原理計算によりAlの4配位と6配位のスペクトルを同定し、深さ方向に配位数が変化していることを見い出しました。
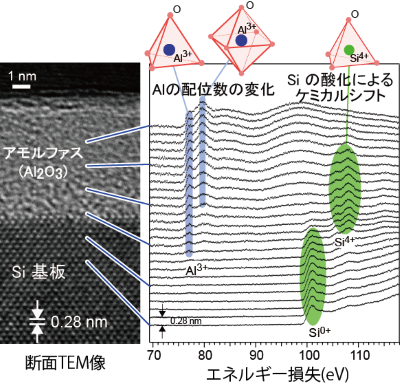
位置分解EELSでは異なるエネルギーの電子線を1次元ではあるものの同時に結像できるので、内殻励起電子による格子縞のコントラストと位置を正確に観察することができます。プラズモンロス電子や内殻電子励起について非弾性散乱過程の非局在性と干渉性を議論しました[Ultramicroscopy 2003]。 非弾性散乱電子も非局在性のために干渉性を保持し、例えば焦点変調により格子縞のコントラストが反転します。つまり明るく光っているところに原子があるとは限りません。当時学会で「非弾性散乱電子が干渉する」と発表をしたところ、興味をもって質問してくれたのは田中通義先生でした(「熱散漫散乱は干渉しますか?」という深い質問でした)。このころからEFTEMで原子分解能を実現することは色収差の観点から原理的に難しいと痛感し、STEMの準備を始めました。
STEM-EELSで初めて原子列を分解してマッピングしました[Nature 2007]。非弾性散乱が局在する内殻励起過程を使うことが重要です。 LaはN殻励起では原子配列は見えないがM殻励起では見えることをデータを示しました。古典的な描像では、外側(例えばN殻)電子が原子位置に局在していないため、入射電子が離れたところを通っても非弾性散乱が起こると考えることができます。あるいは、エネルギー損失が小さい場合には特性角と呼ばれる散乱角が小さく、散乱物体が大きいと考えることもできます。
エネルギー損失が数100eV程度では非局在化因子が空間分解能を制限します。SiのL殻励起(~100eV)は非局在化しており、結晶の原子列は本来識別できません。干渉縞の位置が原子配列に対応しません。ただし、SiのL殻励起でもエネルギー損失値を大きくとることでSTEM-EELSで原子列を分解することができます[Micron 2008]。

実験に使った装置は日立のSTEM専用機(HD-2300C)を徹底的に改造したもので、学会で発表した際には、その変貌した外観[Microscopy 2007]に、営業の人が引いていました。日立の砂子沢さん中村邦康さんや会沢さん曽田さん加藤博さんには大変お世話になりました。Natureへの投稿を勧めてくれたのは末永先生でした。実はこの原子マッピングを実現した装置には球面収差補正装置はついていませんでした。特注の対物レンズや巻き数の少ない高倍率用のコイルを入れてもらい、光軸はエネルギーフィルターで確認しました。小刻みな室温変動を避けるためにエアコンを切った状態で(冬限定)実験をし、計測には1時間かかっていました。試料ホルダーをセットして装置をベーキングしてコンタミを減らして実験していました。
2010年12月、我々も球面収差補正STEM/TEM装置を導入することができました。STEM-EELS分析に1時間もかけなくて良くなりました。装置導入を承認いただいた岸理事長(当時)他幹部の皆様に心よりお礼申し上げます。米国やカナダの国立研究所の施設なども見学し、装置と設置室の仕様を考えました。 電子顕微鏡本体とオペレーター用操作卓とを完全に分離した設置室レイアウト にし、電源安定化装置(電研精機)を屋外に設置し、室内空調は冷却パネル式(日本スピンドル)、アクティブの除振台(特許機器)を設置し、安定度の高い試料ホルダー(メルビル)と、特注のプラズマクリーニング装置(真空デバイス)を導入しました。設置室レイアウトでは長井拓郎さん倉嶋敬次さんに大変お世話になりました。その後、共同研究者が我々の設置室レイアウトを参考に、装置導入していると聞いています。
装置は想定以上の性能を発揮し、治田充貴さんが化学結合状態の原子分解能マッピング[APL 2012]、吉川純さんがリチウム電池の正極材のLi元素マッピング[JPCC 2015]、長井拓郎さんがBi系高温超電導体マッピング[Physica C 2014] などを報告してくださいました。また、1.4.で述べたようにモノクロメーターを用いた低加速高分解能TEM像観察等にも利用しています。グループの原野さん やCretuさんの研究成果もご覧ください。
EELSのエネルギー分解能は電子銃のエネルギー広がりや、分光器あるいは加速電圧の安定度によって決まっています。2000年代前半、私たちは冷陰極電界放出銃(Cold Field Emission Gun, CFEG)電子顕微鏡のエネルギー分解能を上げるために、既設装置(HF-3000+GIF2000)の改造を始めました。高圧電源をシールドをしたり((株)オータマ)、配線のシールドや絶縁トランスの導入などを行いました。当時KrivanekがNIMSに見学に来た時、我々の装置の高圧タンクをノックして加速電圧の揺れを確認していました。
様々な理由でスペクトルのエネルギー値が揺れるため、長時間計測時のエネルギー分解能は劣化するのが常でした。そこで、高速多重計測して計測後にドリフトを補正するプログラムと、low-loss high-loss low-lossの順に3重露光して一度に読みだし、EELSの実効的なエネルギー分解能と精度を向上させました[J.Microsc. 2002]。 同じようなコンセプトがその後(2007年発表のQuantum以降)DualEELSとしてGatan社より製品化されています。同論文ではレフェリーの勧めにしたがってDigitalMicrographのscript例をAppendixに示しました:私の知る限りscriptが掲載された初めての例だと思います。
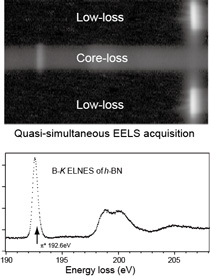
さらに、CCDの読出しの際の際にシャッターを開けたままにしてスペクトルを取得するStreak imagingよりCFEGで0.23eVの最高分解能を実現[Micron 2005] しました。CFEGのエネルギー分解能は物理的にフェルミテールと、トンネリングテールで決まっていることを実験的に明らかにしました。
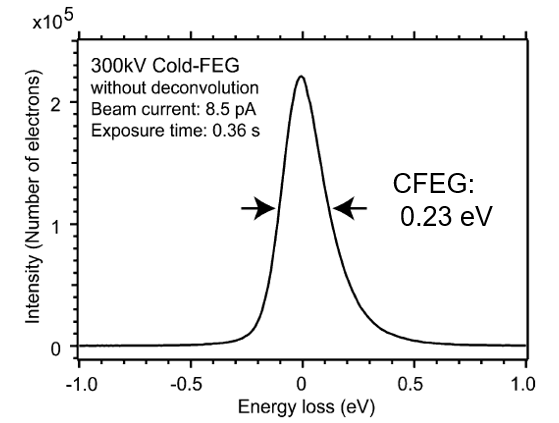
Low-lossとhigh-lossスペクトルを同時に計測することができれば、low-lossスペクトルを装置関数として、high-lossスペクトルをdeconvolutionすることができます。石塚和夫先生がMaximum-Entropy法とRichardson-Lucy法によるdeconvolutionプログラムを作ってくださり[Microscopy 2003]、 それを使ってスペクトルの微細構造を議論できるようになりました。収束を速くするアルゴリズムの工夫もしてくださり、DeConvEELS(HREM Research Inc.)として製品化されています。
0.2eV以下のエネルギー分解能を実現するためには、モノクロメーターが必要です。電子顕微鏡用のモノクロメーターは、2001年にFEI社(現Thermo Fisher Scientific)がはじめて製品化しました。幸いにして2002年、Prof. Hoferの好意により初号機を使う機会に恵まれ、1週間オーストリアのGraz工科大を訪問し、木本と同年代のKothleitnerさんとGroggerさんと一緒に実験しました(ちなみに木本も軸調整を試みましたがそのデータは全滅でした)。Hofer先生から、B.SchafferさんがDigitalMicrographのScriptのデータベースを作っているよと紹介してもらいました。

当時モノクロメーターのエネルギー分解能は0.2eV(半値全幅)で、CFEGの0.23eVと大きく変わりません。しかしCFEGでは避けられないトンネリングテールが、モノクロメーターには無く、これはゼロロスピーク強度を対数表示することで明らかです(Fig. 2.5a)。モノクロメーターの利点がここにあり、バンドギャップ計測に適していることがわかりました。そこで、ピーク強度の1/1000を分解能の指標とすべきであると報告しました[Micron 2005]。 この値はKimoto Limitと呼ばれたこともあります。またCFEGとの比較の図はDB.Williams&CB.Carterの教科書にも引用されました。
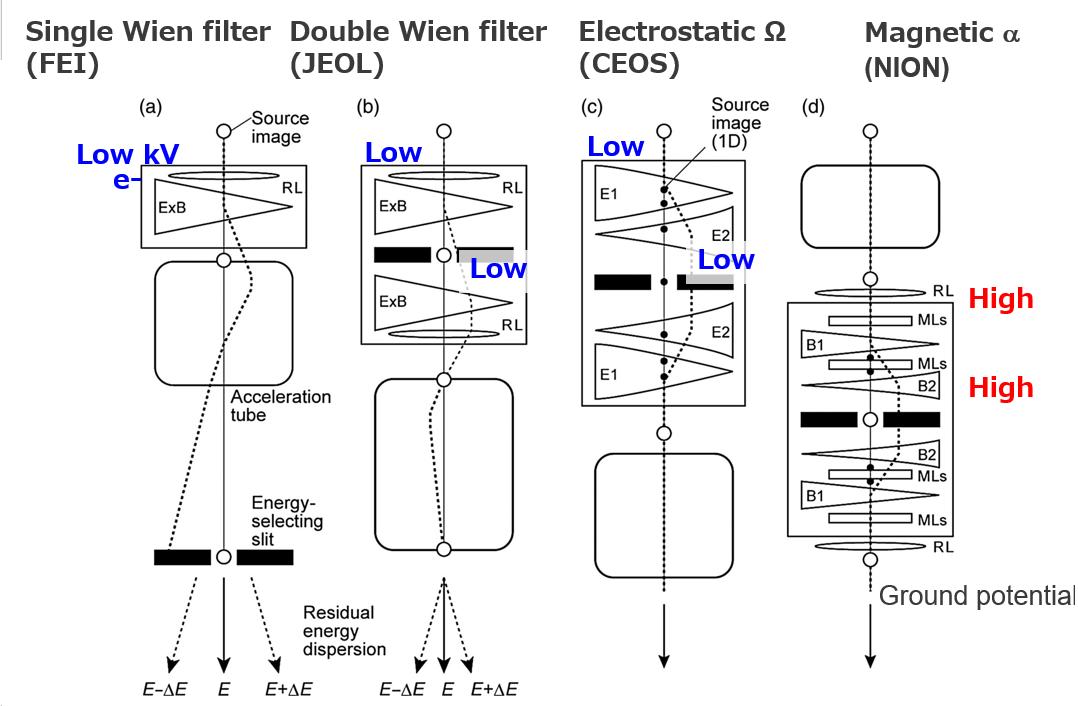
FEIによる製品化発表後、JEOLやCEOS社、NION社もモノクロメーターを製品化しました。それらの模式図と特徴についての解説をMicroscopy誌に執筆しました[Microscopy 2014]。 その模式図は、Hawkes&Spence, Handbook of Microscopy (2019)にも引用されました。分光器内とエネルギー選択スリット上での電子のエネルギーの違いと、最終的に残るエネルギー分散の違いを整理しています。
TEM用のモノクロメーターはエネルギー分解能が向上しており、現在では10 meVを切るエネルギー分解能が報告されています。数100 meVのフォノンの計測の報告が、国内外で行われています。電子顕微鏡グループの吉川純さんは、ダイヤモンドや立方晶窒化ホウ素のフォノンを計測[Kikkawa 2022]をしたり、企業と共同して半導体・絶縁体のギャップ内準位の計測をしています[Yamashita 2024][Asano 2022]。詳しくは吉川純さんの研究内容を参照ください。
STEMでは環状暗視野(annular dark-field, ADF)像や環状明視野像、明視野像など様々な画像を撮影して構造解析できます。特にADF像は、非可干渉性結像とみなすことができ、構造直視性に優れています。ADFの優れた結像特性はS.J.Pennycookらによって1991年に示されました。
STEMの実験を始めた当初、球面収差補正装置もモノクロメーターもなかった我々は、分解能を何とか向上させたいと考えました。非可干渉性結像(incoherent imaging)であれば、EELSと同様に高速多重計測でノイズを低減し、deconvolutionで分解能が向上できるはずだと考えました。そこでEELS用に開発(2002年)したscriptをSTEM用に書き換えました。多重計測により格段にSN比を向上させ、EuドープSiN中のEu単原子の観察に成功しました[APL 2009]。 格子間ドーパントの観察では入射電子のチャンネリングが重要で、シミュレーションとの比較も行い単原子であることを同定しました。単層グラフェンの観察にも用い[Microscopy 2015]、FEIの製品カタログにも使われました。現在高速多重計測はDCFIとして製品化されています。
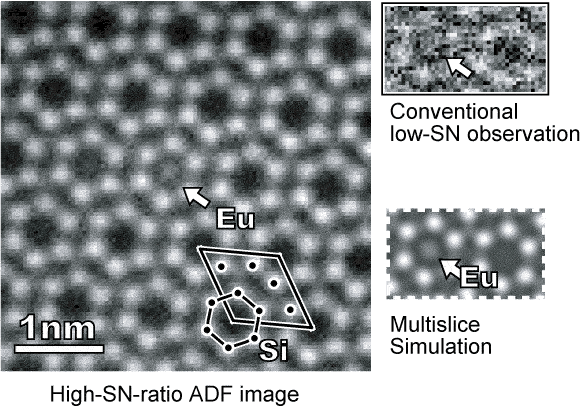
SN比が高ければ、ADF像の輝点位置はEELSのピーク位置と同様に、高精度に決定できるはずです。高SN比画像をMaximum Entropy法などでdeconvolutionすれば原子位置を分解能よりもはるかに高精度に決定できます。高速多重計測機能にさらに対象をトラッキングする機能を追加し、原子位置精度をピコメートルオーダーまで向上させました[Ultramicroscopy 2010]。 また、試料傾斜すると位置確度が低下し、輝点が原子位置に相当しないことなども指摘しています[JEM 2012]。これは、高精度に計測する努力が本当に意味があるのか(言い換えれば、測っても仕方がないものを、時間とお金をかけて測っているような悲喜劇になっていないのか)という観点から、とても重要なことだと思っています。
我々が目指しているのは、極微小領域での結晶構造解析です。ADF像は構造直視性に優れていますが、シミュレーションとの比較ではADF像強度を定量的に計測する必要があります。NIMS九大連携大学院の学生(山下さん)と一緒に、ADF像観察システムの非線形応答特性を正確にキャリブレーションして、 ADF像強度を定量化しました[Microscopy 2015a]。 さらに試料上の光源径を正確に定量することで、原子分解能のグラフェン像をシミュレーションと量子ノイズレベルで一致させ、元素も識別できるようにしました[Microscopy 2015b] 。光源径が実験的に求められたことにより、電子銃の輝度を計測することもできます。

次に われわれはMoS2やWS2の定量化ADF像を観察しました。ADF像は原子番号Zの1.5~1.7乗に比例するいわゆるべき乗則が成り立つと言われているのですが、原子番号が大きくなると成り立たなくなっていました [Sci. Rep. 2018] 。 これは単原子でも第一ボルン近似が破綻していることを示しています。正確・精密・慎重に計測した結果、それまでの理論と異なる結果が出た時、それは驚きとともに新規な研究成果や方向性を我々に示してくれます。
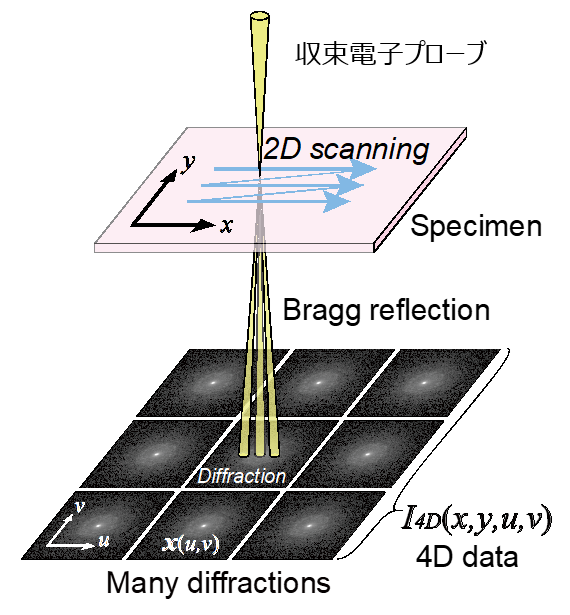
電子プローブを試料上で2次元走査しながら、回折図形(2D)を撮影して4次元データを取得する手法は、2019年Ophusが4D-STEMと命名しまRutherford scatteringて原子分解能を報告しました[Ultramicroscopy 2011]。ちなみに我々はspatially-resolved diffractometryと呼んだのですが、まったく普及しませんでした。この論文では計測後に様々な(BF, ABF, LAADF, MAADF, HAADF)STEM画像が構築できることに加え、Rutherford scattering様の散乱を実空間で明らかにしました。
.png)
さらに得られた計測データをいわゆるビックデータとみなし、教師なし 機械学習(次元削減やクラスタリング)と組み合わせました[Ultramicroscopy 2021]。 次元削減では主成分分析(Principal Component Analysis, PCA)が広く知られていますが、我々は非負値行列因子分解(Nonnegative Matrix Factorization, NMF)を使っています。PCAは多次元データから特徴抽出する代表的な手法ですが、要素に負値が含まれるため、回折図形として解釈できないという問題があります。他方NMFは計算負荷が高く、局所解に収束する可能性もありますが、解釈可能な結果を与えてくれる点で実験データ解析に適しています。上杉さんと協力し、2021年まずはTiO2に対する実験結果に対して、DigitalMicrographのscriptでNMFを実行しました。NMFには、Alternating Least-Squares (ALS) algorithmやMultiplicative Update (MU) algorithmが知られています。我々はそれらのalgorithmを使うとともに、PCAとも比較しながら計算負荷や収束を確認しています。金属ガラス[Sci.Rep.2024]や単層MoS2 [Small Methods 2025]へも適用しています。大量の回折図形データから有益な情報を抽出することが可能です。
NMFで得られた結果は、常に計測結果として解釈できるわけではなく、artefactが生じることが知られています。 我々はNMFで見られるartefactを避けるため、電子回折図形としてありえない強度変化を禁じる拘束条件をALSアルゴリズムに組み込みました(constrained NMF) [Sci. Rep 2025]。その結果、アモルファス中の結晶性析出物の精確な分離が可能になりました。
計測研究者は多くの場合、残念ながら情報科学については最先端ではありません。しかし私たちは計測機器に出来合いのデータ解析ソフトウエアを組み合わせるだけで「計測インフォマティクス研究」になるとは考えていません。情報科学の分野でも、分野固有の知識(domain-specific knowledge)は重要と認識されているようです。計測インフォマティクスで最先端となるためには、電子回折散乱・電子光学・計測装置・物質材料等に関する知識をどれだけ組み込めるかが重要だと思っています。 先端研究者が計測科学・技術を踏まえているのと同様に、情報科学についてもできるだけ非ブラックボックス化したいと思っています。情報科学・ソフトウエア工学については、今後も専門家に教えを請い、あるいは共同して研究していきたいと考えています。 今後計測機器の進歩により得られる計測データは増大し、情報科学(informatics)との融合、すなわち計測インフォマティクスはますます進むことが期待 されます。
物質材料中の微細構造が巨視的な物性やデバイスの性能を決定する例は数えきれないほどあります。例えば鉄鋼などの構造材料の機械的強度は結晶粒子径や析出物あるいは欠陥によって決まっており、半導体・磁性デバイスは異種材料の界面状態により特性が左右されます。カーボンナノチューブは透過電子顕微鏡の専門家である飯島先生によりTEM観察中に発見されました。透過電子顕微鏡は多様な微細構造解析手法を提供し、物質材料研究に大いに貢献してきました。
透過電子顕微鏡観察をしていると、 ミクロな構造に加えてより概念的に大きなものが見えてくることがあります。 例えば予想していなかった微細構造や原子配列が見えることで、新たな物質科学や材料工学など、本質的なものが見え、新発想を喚起する可能性があります。 透過電子顕微鏡により見出した予想外の物質・構造・現象が、論文発表やプレスリリースではあたかも「それを目指して研究開発に成功」「新概念を提案」とされるされる場面に、研究者はしばしば遭遇してきました。セレンディピティーの本質であり、材料イノベーションの典型的な一例とも言えます。先端計測技術は、マテリアル革新力強化のためのテクノロジーブースターの役割を果たしうると思います。
電子顕微鏡による計測・解析のために、DititalMicrograph(DM)のscriptを使っています。詳細は[DM入門] をご覧ください。
「物質・材料研究のための透過電子顕微鏡(講談社 2020)」を、木本・三石・三留・原・長井の5名で上梓しました。目次等は[TEM入門] をご覧ください。
共同研究者およびご指導いただきました先生方に感謝いたします。すべての方のお名前をあげられないことをお詫びします(順不同敬称略)。美浜和弘・田中信夫(名大)・田中通義(東北大)・十倉好紀(東大)・田中功(京大)・砂子沢成人・谷口佳史・宇佐美勝久・平野辰巳・鍛示和利・中村邦康・曽田晃平・加藤博・屋久四男・成重慎治・二本正昭・平山義幸・星屋裕之・永田文男(日立)・沢田英敬・佐々木健夫(JEOL)・松本良平・鈴木篤司(日本エフイー・アイ)・堀内繁雄・松井良夫・板東義雄・鶴田忠正・柳澤圭一・佐々木高義・谷口尚・廣崎尚登・吉川純・原野幸治・川本直幸・Han Zhang・Ovidiu Cretu・長井拓郎・小原真司・東後篤史・三石和貴・三留正則・原徹・倉嶋敬次・上杉文彦・大和田めぐみ・治田充貴(現京大)・長尾全寛(現名大)・山下俊介(現SONY)・越谷翔悟(現JEOL)・斎藤光浩(現JEOL)・肖英紀(現秋大)、浅香透(現名工大)・吉村巧己・魚田将史(DIC)・于秀珍(現RIKEN)・平田秋彦(早大)・志賀元紀(東北大)・大島義文・麻生浩平(JAIST)・金子賢治(九大)・田中考治(AIST)・佐伯哲平・伊野家浩司・高内幸一(Gatan)・細川史生(FH electron optics)・陰山洋(京大)・前田和彦(東京科学大)・大谷亮(九大)・寺内正己(東北大)・幾原雄一(東大)・倉田博基(京大)・末永和知(阪大)・溝口照康(東大)・石塚和夫・石塚顕在(HREM Research Inc.), O.L. Krivanek, R.F. Egerton, M. Malac, B. Freitag, E.v.Cappellen, S.Lazar, A.Bright, F. Hofer, G. Kothleitner, W. Grogger, C. Trevor, J. Hunt, M. Barfels, R. Twesten, M. Rabara, R.E. Dunin-Borkowski, et al.