Abstract
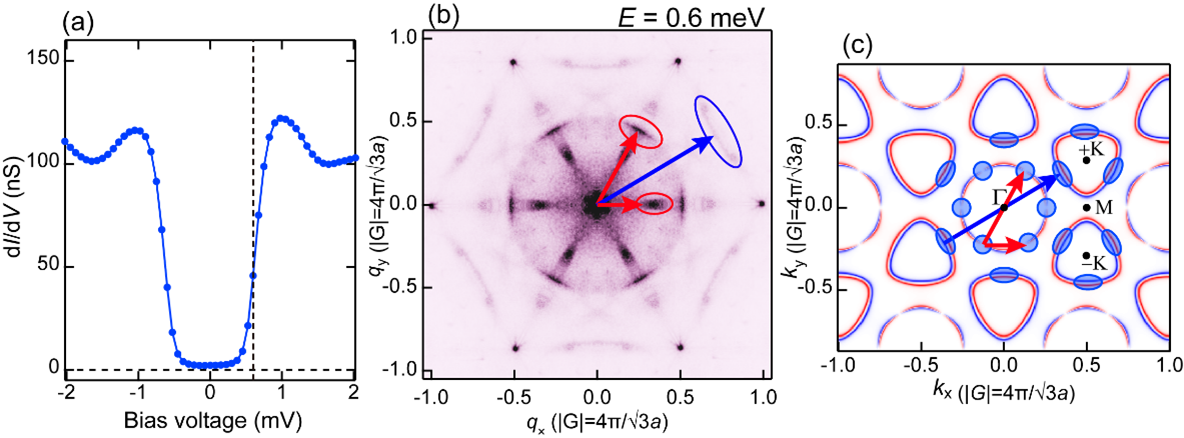
Transition metal dichalcogenide (TMD) superconductors are known for hosting a variety of exotic superconducting phenomena, such as Ising superconductivity [1], orbital Fulde-Ferrell-Larkin-Ovchinnikov states [2], and pair-density waves (PDWs) [3]. In particular, understanding the origin of PDWs requires detailed insight into how coexisting charge density waves (CDWs) influence the superconducting gap structure. As a crucial first step, it is essential to elucidate the superconducting gap structure in systems free from CDW interference. In this study, we focus on 2H-NbS2, a TMD superconductor that does not exhibit CDW order, and perform Bogoliubov quasiparticle interference (QPI) measurements using a dilution-refrigerator-based scanning tunneling microscope (STM) with an energy resolution of ~20 μeV [4]. The tunneling spectra measured at 90 mK reveal broad superconducting gaps indicative of multiple anisotropic gap structures [Fig. 1(a)]. Additionally, the QPI pattern measured at 0.6 meV, where the superconducting gap becomes its minimum, exhibits localized QPI spots arising from gap anisotropy [Fig. 1(b)]. These spots correspond to scattering vectors connecting between the Fermi surface segments indicated by the blue ellipses in Fig. 1(c), suggesting that the superconducting gap is minimized at these points. While the observed anisotropy around the Γ-centered Fermi surface is consistent with theoretical calculations based on the momentum-dependent electron-phonon coupling, the anisotropy observed near the K-centered Fermi surface is reverted from these predictions [5]. These results suggest that mechanisms beyond conventional electron-phonon interactions may play an essential role in the superconductivity of this system.