


�$B meanings of the excess
�$B>e$X�(B: , another (easier) derivation
�$BLa$k�(B: , another (easier) derivation
How to solve
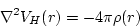 |
(218) |
when
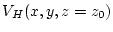 and
and
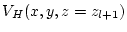 are given.
are given.
split
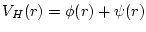 ,
,
where 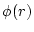 is the solution of the Poission equation
with charge
is the solution of the Poission equation
with charge 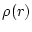 without any boundary condition
in the region from
without any boundary condition
in the region from 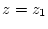 to
to 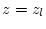 .
.
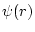 is the solution of the Poission equation
without charge and with the boundary condition
is the solution of the Poission equation
without charge and with the boundary condition
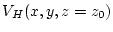 and
and
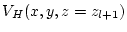 in the region from
in the region from 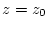 to
to 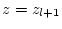 .
.
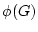 , the Fourier transform of
, the Fourier transform of 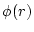 , can be solved in the usual way for periodic boundary condition as
, can be solved in the usual way for periodic boundary condition as
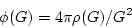 |
(222) |
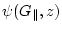 can be solved analytically using the formula of the previous chapter
with the condition
can be solved analytically using the formula of the previous chapter
with the condition 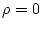 . Surely eq.(210) has such a form.
. Surely eq.(210) has such a form.
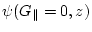 can be also solved using the formula of the previous chapter
with the condition
can be also solved using the formula of the previous chapter
with the condition 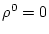 .
The solution, eq(221), is simply,
.
The solution, eq(221), is simply,
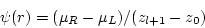 |
(223) |



�$B meanings of the excess
�$B>e$X�(B: , another (easier) derivation
�$BLa$k�(B: , another (easier) derivation
kino
�$BJ?@.�(B18�$BG/�(B4�$B7n�(B17�$BF|�(B
![]() ,
,
![]() , the Fourier transform of
, the Fourier transform of ![]() , can be solved in the usual way for periodic boundary condition as
, can be solved in the usual way for periodic boundary condition as