


�$B derivation 2. time-independent
�$B>e$X�(B: current
�$BLa$k�(B: current
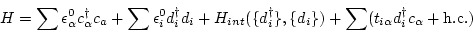 |
(107) |
current from L region is
![\begin{displaymath}
J_L = - (-e) \langle \dot{N}_L \rangle = i e \langle [ H, N_L ] \rangle
\end{displaymath}](img252.png) |
(108) |
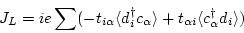 |
(112) |
interesting that the prefactor of the current is imaginary!
Define Keldysh Green functions
Dyson equation,
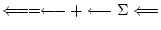 , reads
, reads
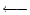 means non-interactiong Green function and is diagonal.
means non-interactiong Green function and is diagonal.
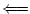 means interactiong Green function which includes
self-energies.
means interactiong Green function which includes
self-energies.
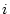 is indexes in the region C and
is indexes in the region C and 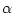 is in the region L, e.g.,
is in the region L, e.g.,
and so on.
The second term reads
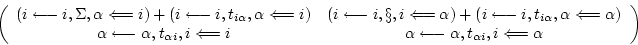 |
(119) |
The (2,1) component of eq.(118) gives
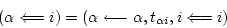 |
(120) |
Thus for equilibrium Green functions,
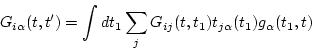 |
(121) |
For non equilibrium Green functions,
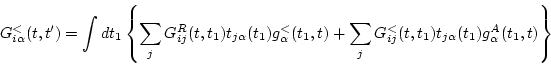 |
(122) |
time dependence of
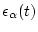
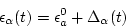 |
(123) |
In the stochastic approximation,
return to eq.(113),
5
See also the Appendix.
Use eq.(123), eq.(125) and eq.(126)
insert
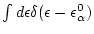
Define
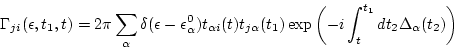 |
(131) |
Then
![\begin{displaymath}
\sum_{\alpha i} t_{\alpha i} G_{i \alpha }^<(t,t) =
i \sum_...
...f(\epsilon _\alpha ^0) + G_{ij}^<(t,t_1) \theta(t-t_1) \right]
\end{displaymath}](img295.png) |
(132) |
Taking into account of
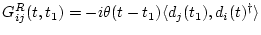 ,
upper limit of
,
upper limit of 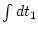 is
is 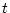 .
.
![\begin{displaymath}
\sum_{\alpha i} t_{\alpha i} G_{i \alpha }^<(t,t) =
i \sum_...
...
\left[ G_{ij}^R(t,t_1) f(\epsilon ) + G_{ij}^<(t,t_1) \right]
\end{displaymath}](img299.png) |
(133) |
Therefore
![\begin{displaymath}
J_L(t) = 2 e \int_{-\infty}^{t} d t_1 \int \frac{d\epsilon }...
...amma(e,t_1,t) ( G^R(t,t_1) f(\epsilon ) + G^<(t,t_1))
\right]
\end{displaymath}](img300.png) |
(134) |



�$B derivation 2. time-independent
�$B>e$X�(B: current
�$BLa$k�(B: current
kino
�$BJ?@.�(B18�$BG/�(B4�$B7n�(B17�$BF|�(B
![]() , reads
, reads
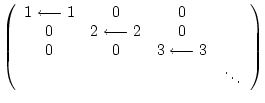
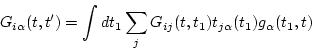
![]()
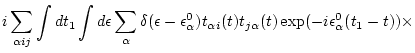
![$\displaystyle \exp \left( -i \int_{t_1}^{t} d t_2 \Delta_\alpha (t_2) \right)
\...
...
G_{ij}^R(t,t_1) f(\epsilon _\alpha ^0) + G_{ij}^<(t,t_1) \theta(t-t_1) \right]$](img293.png)
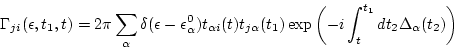
![\begin{displaymath}
\sum_{\alpha i} t_{\alpha i} G_{i \alpha }^<(t,t) =
i \sum_...
...f(\epsilon _\alpha ^0) + G_{ij}^<(t,t_1) \theta(t-t_1) \right]
\end{displaymath}](img295.png)
![\begin{displaymath}
\sum_{\alpha i} t_{\alpha i} G_{i \alpha }^<(t,t) =
i \sum_...
...
\left[ G_{ij}^R(t,t_1) f(\epsilon ) + G_{ij}^<(t,t_1) \right]
\end{displaymath}](img299.png)