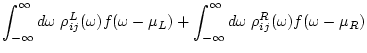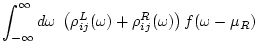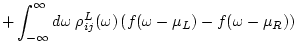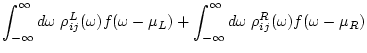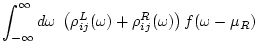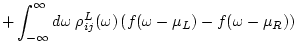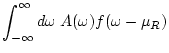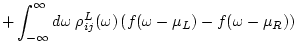�$B current
�$B>e$X�(B: total charge
�$BLa$k�(B: in the non-equilibrium
From eqs.(90) and (95),
Assuming 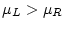 ,
we can replace
,
we can replace
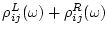 with
with 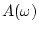 for
for
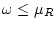 .
.
We evaluate the first term in eq.(81).
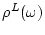 in the second term is not analytical.
in the second term is not analytical.
kino
�$BJ?@.�(B17�$BG/�(B12�$B7n�(B15�$BF|�(B