層状マンガン酸化物Nd1-xCa1+xMnO4の電荷軌道整列構造の解析
長井拓郎
巨大磁気抵抗効果(CMR効果)を示すことで知られるマンガン酸化物で電荷軌道整列現象が見いだされ、現在、精力的に研究がなされています。この電荷軌道整列状態において形成される結晶学的超構造の解析は、その電荷と軌道の配列パターンを解明する上で大変重要です。最近、私達のグループは、214型層状マンガン酸化物Nd
Nd1-xCa1+xMnO4(0.55≦x≦1)多結晶試料をメノウ乳鉢で粉砕し、四塩化炭素中に超音波分散させた後、上澄み液をカーボンマイクログリッド上に滴下して電顕観察試料を作製しました。室温および極低温における電子回折測定および高分解能像観察には、液体窒素冷却ホルダー(Oxford CHDT 3504)を備えた電界放出型透過型電子顕微鏡Hitachi HF-3000S(加速電圧300kV)を用いました。
図1に[001]入射で得られた組成x=0.69の電子回折図形((a) 340K, (b) 80K)を示します。80Kでは基本反射に加え一連の明瞭な超格子反射が出現しているのが分かります。この超格子反射は0.55≦x≦0.75の組成、つまり、格子に対して整合および不整合となるeg 電子濃度(0.25≦ne≦0.45)で出現しました。超構造の変調波数ベクトルは組成xを用いてq=[1-x,0,0]と表すことができます。これは214型層状マンガン酸化物Nd1-xSr1+xMnO4や113型擬立方構造をもつLa1-xCaxMnO3における関係と等価です。1)-2)
この系の超構造を明らかにするために、80Kにおける高分解能電子顕微鏡観察を行いました。図2に80Kにおいて[001]入射で得られた高分解能像((a) x=2/3 (ne=1/3)、(b) x=0.7 (ne=1/3.3))を示します。eg電子濃度が格子に対して整合する組成x=2/3 (ne=1/3)では、a軸方向に基本周期に整合した3aの周期をもつ正弦波的な横波の構造の変調およびなだらかに変化する超格子干渉縞が観察されました。この観察結果から横波正弦波の原子変位をもつ超構造モデルを構築し電子回折図形および高分解能像のシミュレーションを行ったところ、実験結果を正確に再現することができました。そして、eg電子濃度が格子に対して不整合となる組成x=0.7 (ne=1/3.3)では、a軸方向に基本周期に整合しない3.3aの周期をもつ正弦波的な横波の構造の変調および同様の超格子干渉縞が観察されました。この場合の超構造モデル図を図3に示します。このような不整合変調構造では今までに提案された「Wigner-crystal」モデル1) 等のeg電子がMnサイトに固定されたモデルでは解釈することはできません。ここで新たにeg電子の電荷と軌道状態の連続的な変調を考える必要があります。eg電子の軌道状態は擬スピン空間において次式により表すことができます。
|θi>=cos(θi/2)|x2-y2>+sin(θi/2)|3z2-r2>
このマンガン酸化物における軌道状態の変調は擬スピン空間におけるθがπ/3と-π/3との間を連続的に変化する、つまり3x2-r2軌道と3y2-r2軌道の間で連続的に移り変わるものであると考えられます。この軌道の変調は軌道密度波に相当するものです。そしてθがπ/3および-π/3をとる位置で電子密度が最大となるような電荷密度の変調(電荷密度波)が存在すると考えられます。
この研究により、電荷軌道整列状態のマンガン酸化物における「電荷密度波」および「軌道密度波」の存在の可能性が示唆されました。
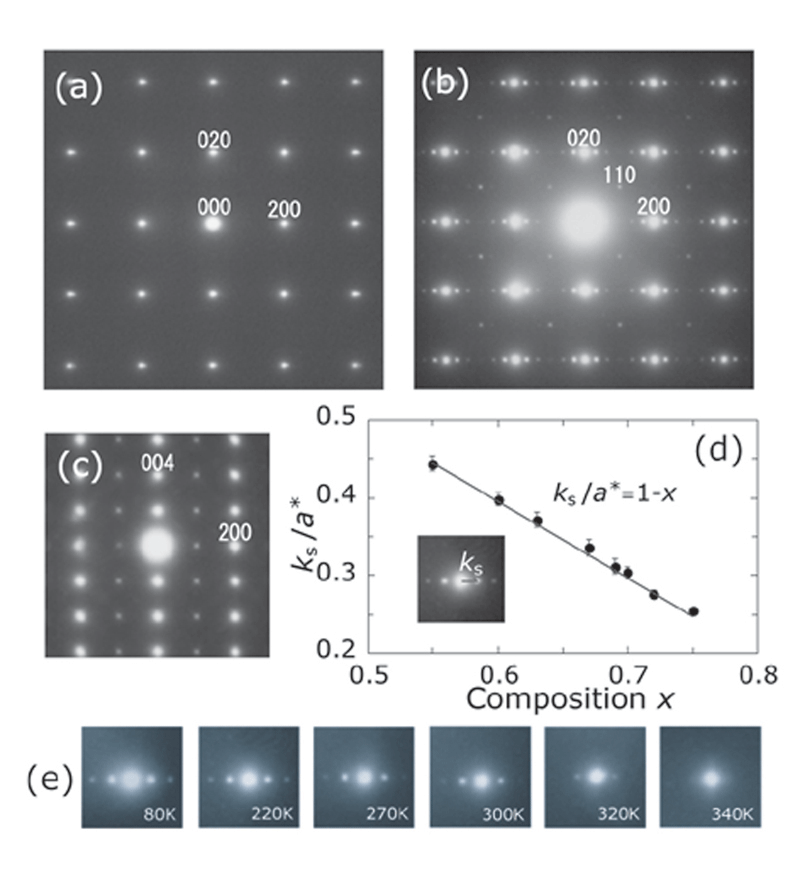
Fig. 1: (a)-(c) Electron diffraction patterns of Nd1-xCa1+xMnO4 (x=0.69) (a) at 340K (>TCO) along [001], (b) at 80K (<TCO) along [001], and (c) 80K (<TCO) along [010]. The hk0 (h, k: odd number) reflections are fundamental ones of the low-temperature Pccn structure. (d) The relationship between the propagation vector of the superstructure ks and the composition x. (e) Temperature dependence of the superlattice reflection intensity for x=2/3.
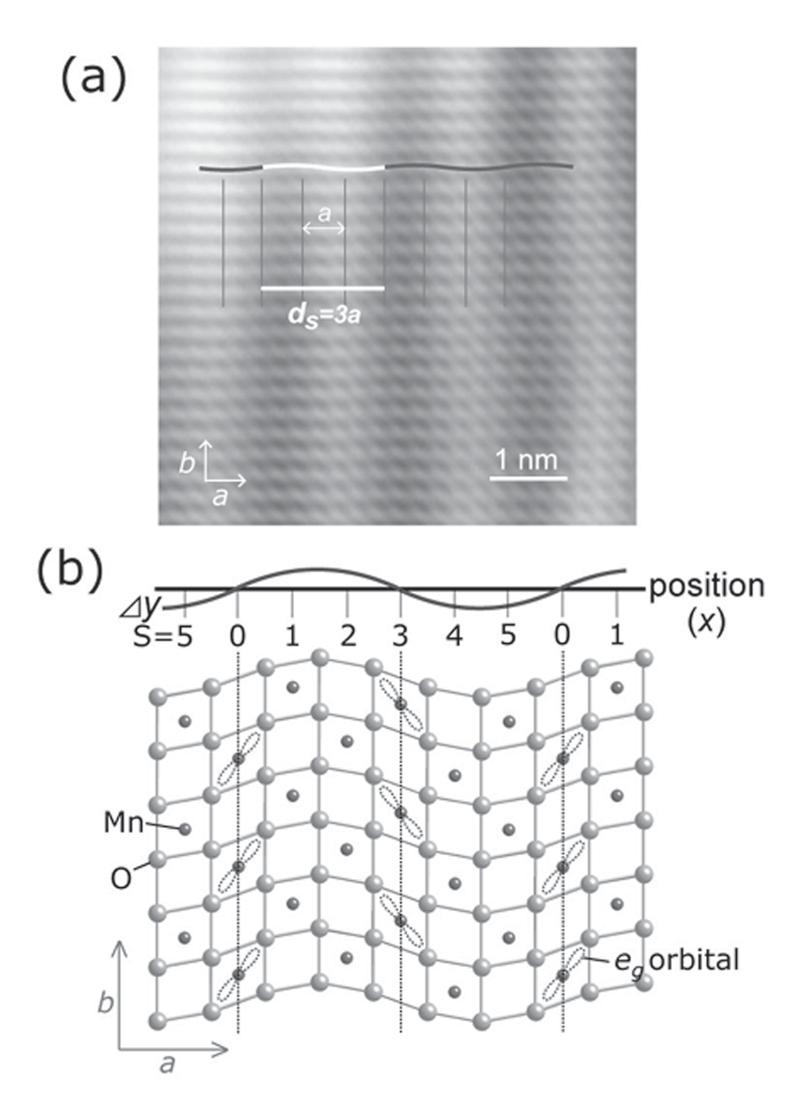
Fig. 2: (a) HREM image taken along the [001] direction at 80K (<TCO) for x=2/3. (b) Proposed superstructure model for x=2/3. In order to simplify the drawing, only one of MnO2 plane is shown, and the transverse atomic displacement is exaggerated in the fugure.
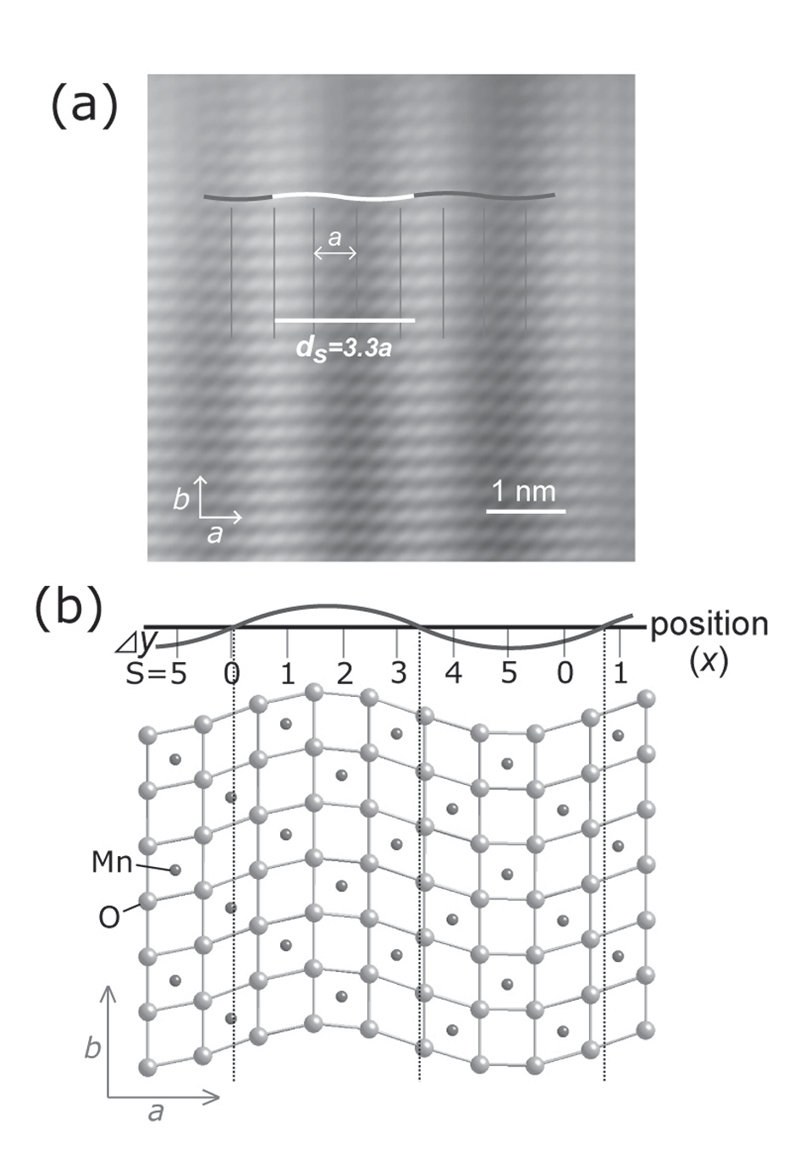
Fig. 3: (a) HREM image taken along the [001] direction at 80K (<TCO) for x=0.7. (b) Proposed superstructure model for x=0.7.
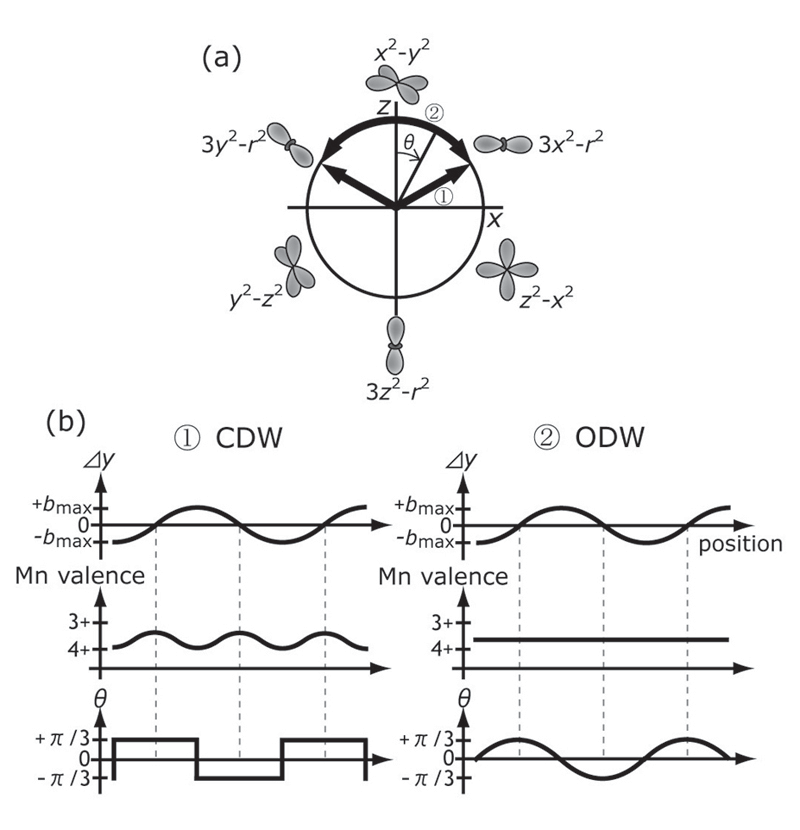
Fig. 4 : (a) Schematic picture of the eg orbital state by the psuedo-spin space. θ=-π/3, 0, and π/3 correspond to 3y2-r2, x2-y2, and 3x2-r2 orbital state, respectively. (b) Mn valence (or electron density) and θ as a function of position (along the direction vertical to stripe) in the charge density wave state (left) and the orbital density wave state (right).