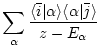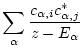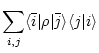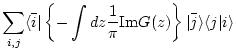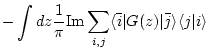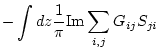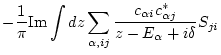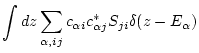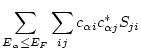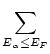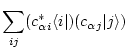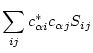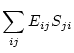charge density in the non-orthogonal basis set

In this section, we consider the dual basis representation.

Eigen value and eigen state safisfy the equation,

$$H \vert \alpha \rangle = E_\alpha \vert \alpha \rangle$$

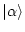$\vert \alpha \rangle$ is constructed using atomic basis set 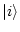$\vert i\rangle$ (LCAO),

$$\vert \alpha \rangle = \sum_i c_{\alpha, i} \vert i\rangle$$

The eigen energy is calculated by solving generalized eigenvalue problem,

$$\langle i \vert H \vert j \rangle = E \langle i \vert j \rangle$$ (276)

$$H_{ij} = E S_{ij}$$ (277)

with the normalization condition 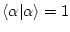. The Green function is defined as

$$G(z) = \sum_{\alpha} \frac{ \vert \alpha \rangle \langle \alpha \vert }{ z-E_\alpha}$$

Here we define the dual basis set in the atomic basis set,

$$\vert \bar{i} \rangle = \sum_j \vert j \rangle S_{ji}^{-1}$$

where 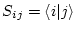. Then

$$\langle \bar{i} \vert j \rangle = \delta_{ij}$$

The trace of 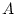$A$ is expressed as

$$\mbox{Tr}[ A ] = \langle A \rangle = \langle \bar{i} \vert A \vert i \rangle$$

The Green function is

$$\langle \bar{i} \vert G \vert \bar{j} \rangle = \sum_{\alpha} \frac{\langle \bar{i} \vert \alpha \rangle \langle \alpha \vert \bar{j} \rangle }{z-E_\alpha}$$ (278)

$$= \sum_{\alpha} \frac{c_{\alpha, i} c_{\alpha, j}^* }{z-E_\alpha}$$ (279)

Then the charge density is

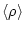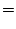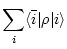$$\langle \rho \rangle = \sum_i \langle \bar{i} \vert \rho \vert i \rangle$$ (280)

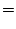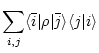$$= \sum_{i,j} \langle \bar{i} \vert \rho \vert \bar{j} \rangle \langle j \vert i \rangle$$ (281)

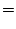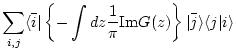$$= \sum_{i,j} \langle \bar{i} \vert \left\{-\int dz \frac{1}{\pi} {\rm Im} G(z) \right\} \vert \bar{j} \rangle \langle j \vert i \rangle$$ (282)

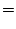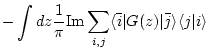$$= -\int dz \frac{1}{\pi} {\rm Im} \sum_{i,j} \langle \bar{i} \vert G(z) \vert \bar{j} \rangle \langle j \vert i \rangle$$ (283)

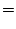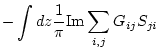$$= -\int dz \frac{1}{\pi} {\rm Im} \sum_{i,j} G_{ij} S_{ji}$$ (284)

Consider the simple case,

$$\langle \rho \rangle = -\frac{1}{\pi} {\rm Im} \int dz \sum_{\alpha,ij} \frac{c_{\alpha i} c_{\alpha j}^* }{z-E_\alpha+i\delta} S_{ji}$$ (285)

$$= \int dz \sum_{\alpha,ij} c_{\alpha i} c_{\alpha j}^* S_{ji} \delta( z-E_\alpha)$$ (286)

$$= \sum_{E_\alpha \le E_F} \sum_{ij} c_{\alpha i} c_{\alpha j}^* S_{ji}$$ (287)

$$= \sum_{E_\alpha \le E_F}$$ (288)

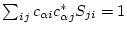because of the normalization of 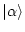$\vert \alpha \rangle$. The left hand side of 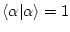can be written as

$$\langle \alpha \vert \alpha \rangle = \sum_{ij} ( c_{\alpha i}^* \langle i \vert) ( c_{\alpha j} \vert j \rangle )$$ (289)

$$= \sum_{ij} c_{\alpha i}^* c_{\alpha j} S_{ij}$$ (290)

The total band energy can be calculated similarly

$$\langle E \rangle = \sum_i \langle \bar{i} \vert E \vert i \rangle$$ (291)

$$= \sum_i \langle \bar{i} \vert E \vert \bar{j} \rangle \langle j \vert i \rangle$$ (292)

$$= \sum_{ij} E_{ij} S_{ji}$$ (293)