


�$B If site0 and site1
�$B>e$X�(B: an 1D chain
�$BLa$k�(B: an 1D chain
Assume that
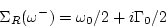 |
(231) |
where
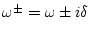 .
.
Then
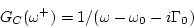 |
(236) |
conductance is
where 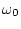 and
and 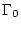 are functions of
are functions of 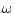 and must be calculated.
and must be calculated.
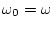 in the range from
in the range from 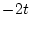 to
to 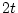 also from numerical calculations.
Therefore
also from numerical calculations.
Therefore 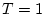 from
from 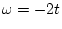 to
to 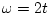 ,
and
,
and
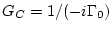 .
.



�$B If site0 and site1
�$B>e$X�(B: an 1D chain
�$BLa$k�(B: an 1D chain
kino
�$BJ?@.�(B18�$BG/�(B4�$B7n�(B17�$BF|�(B