


�$B some examples
�$B>e$X�(B: , another (easier) derivation
�$BLa$k�(B: add boundary condition without
How to solve
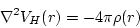 |
(224) |
when
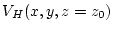 and
and
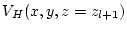 are given.
are given.
Define a parameter, which means the excess charge,
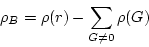 |
(225) |
Then
Eq.(228) is solved via FFT,
while Eq.(229) is solved analytically,
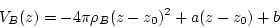 |
(229) |
parameter 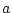 and
and 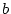 is determined via boundary condition.
The sign of
is determined via boundary condition.
The sign of 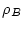 determines how
determines how 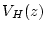 drops. (See figure.1.)
drops. (See figure.1.)
Note that the condition of no s-d bias voltage is satisfied,
even if there exists some excess charge,
�$B?^�(B 1:
relationship between 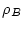 and
and 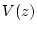
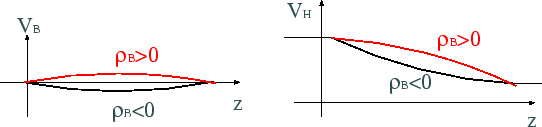 |



�$B some examples
�$B>e$X�(B: , another (easier) derivation
�$BLa$k�(B: add boundary condition without
kino
�$BJ?@.�(B18�$BG/�(B4�$B7n�(B17�$BF|�(B