


�$B use transfer matrix
�$B>e$X�(B: surface Green function, non-orthogonal
�$BLa$k�(B: surface Green function, non-orthogonal
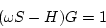 |
(159) |
![\begin{displaymath}
H = \left[ \begin{array}{ccccc}
H_{00} & H_{01} & 0 & 0 & 0...
...& \ddots \\
0 & 0 & 0 & \ddots & \ddots
\end{array} \right]
\end{displaymath}](img32.png) |
(160) |
![\begin{displaymath}
S = \left[ \begin{array}{ccccc}
S_{00} & S_{01} & 0 & 0 & 0...
...& \ddots \\
0 & 0 & 0 & \ddots & \ddots
\end{array} \right]
\end{displaymath}](img352.png) |
(161) |
![\begin{displaymath}
G = \left[ \begin{array}{ccccc}
G_{00} & G_{01} & G_{02} & ...
... & & & G_{33} \\
\vdots & & & & \ddots
\end{array} \right]
\end{displaymath}](img353.png) |
(162) |
Use 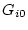 column,
column,
The last two eqs are generalized as
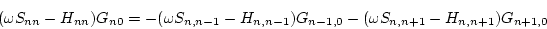 |
(167) |
rewrite the relation between the neighboring site.
The relationship between the second neighboring is
And
the relation between 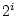 th neighboring layer is
th neighboring layer is
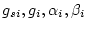 can be evaluated iteratively
can be evaluated iteratively
especially
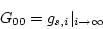 |
(179) |



�$B use transfer matrix
�$B>e$X�(B: surface Green function, non-orthogonal
�$BLa$k�(B: surface Green function, non-orthogonal
kino
�$BJ?@.�(B18�$BG/�(B4�$B7n�(B17�$BF|�(B
![\begin{displaymath}
H = \left[ \begin{array}{ccccc}
H_{00} & H_{01} & 0 & 0 & 0...
...& \ddots \\
0 & 0 & 0 & \ddots & \ddots
\end{array} \right]
\end{displaymath}](img32.png)
![\begin{displaymath}
S = \left[ \begin{array}{ccccc}
S_{00} & S_{01} & 0 & 0 & 0...
...& \ddots \\
0 & 0 & 0 & \ddots & \ddots
\end{array} \right]
\end{displaymath}](img352.png)
![\begin{displaymath}
G = \left[ \begin{array}{ccccc}
G_{00} & G_{01} & G_{02} & ...
... & & & G_{33} \\
\vdots & & & & \ddots
\end{array} \right]
\end{displaymath}](img353.png)
![]() column,
column,
![]() th neighboring layer is
th neighboring layer is
![]() can be evaluated iteratively
can be evaluated iteratively