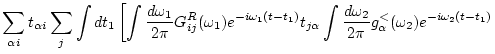 |
|||
![$\displaystyle +
\left.
\int \frac{d \omega _1}{2 \pi} G_{ij}^<(\omega _1) e^{-i...
...\frac{d \omega _2}{2 \pi} g_\alpha ^A(\omega _2) e^{-i\omega _2(t-t_1)}
\right]$](img303.png) |
(135) | ||
![$\displaystyle \sum_{\alpha i j} t_{\alpha i}t_{j\alpha } \int \frac{d \omega _1...
..._1) g_\alpha ^<(\omega _1) + G_{ij}^<(\omega _1) g_\alpha ^A(\omega _1) \right]$](img304.png) |
(136) |
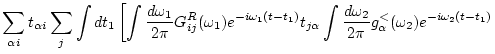 |
|||
![$\displaystyle +
\left.
\int \frac{d \omega _1}{2 \pi} G_{ij}^<(\omega _1) e^{-i...
...\frac{d \omega _2}{2 \pi} g_\alpha ^A(\omega _2) e^{-i\omega _2(t-t_1)}
\right]$](img303.png) |
(135) | ||
![$\displaystyle \sum_{\alpha i j} t_{\alpha i}t_{j\alpha } \int \frac{d \omega _1...
..._1) g_\alpha ^<(\omega _1) + G_{ij}^<(\omega _1) g_\alpha ^A(\omega _1) \right]$](img304.png) |
(136) |
time independent ![]()
![]() (eigenvalue of the isolated L region)
(eigenvalue of the isolated L region)
Green functions become
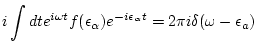 |
(137) | ||
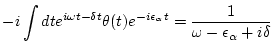 |
(138) | ||
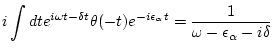 |
(139) |
![]() becomes
becomes
![$\displaystyle 2e {\rm Re} \sum_{\alpha ij} t_{\alpha n} t_{m\alpha } \int \frac...
... _1) +
G_{ij}^<(\omega _1) \frac{1}{\omega -\epsilon _\alpha -i\delta } \right]$](img314.png) |
(140) | ||
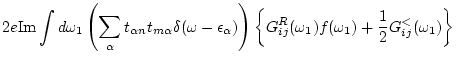 |
|||
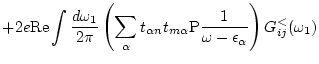 |
(141) |
Here define
| (142) | |||
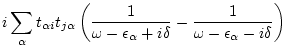 |
(143) | ||
| (144) | |||
| (145) |
Use
![]() ,
,
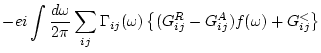 |
|||
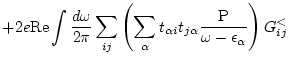 |
(146) |
If region described by ![]() ,
,![]() is non-interacting,
then
is non-interacting,
then
![]() is pure imaginary.
is pure imaginary.
![$\displaystyle -e i \int \frac{d \omega }{2\pi} {\rm Tr}\left[ \Gamma(\omega ) \left\{
(G^R -G^A) f(\omega ) + G^< \right\} \right]$](img328.png) |
(147) |
Let's connect L-C-R.
Use equations,
| (152) | |||
| (153) | |||
![$\displaystyle \frac{e}{2i} \int \frac{d\omega }{2\pi} {\rm Tr} \left[
\Gamma_L (G^R-G^A) f_L + \Gamma_L G^<
- \Gamma_R (G^R-G^A) f_R - \Gamma_R G^< \right]$](img343.png) |
(154) | ||
![$\displaystyle \frac{e}{2i} \int \frac{d\omega }{2\pi} {\rm Tr} \left[
(\Gamma _...
... G^A +
i(\Gamma _R -\Gamma _L) G^R (f_L \Gamma _L + f_R \Gamma _R ) G^A \right]$](img344.png) |
(155) | ||
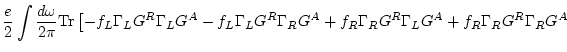 |
|||
| (156) | |||
![$\displaystyle -\frac{e}{2} \int \frac{d\omega }{2\pi} {\rm Tr} \left[
(f_L-f_R) (\Gamma _L G^R \Gamma _R G^A ) + (f_L-f_R)(\Gamma _R G^R \Gamma _L G^A) \right]$](img347.png) |
(157) | ||
![$\displaystyle - \frac{e}{2\pi} \int d\omega {\rm Tr} \left[ (f_L-f_R) (\Gamma _L G^R \Gamma _R G^A )
\right]$](img348.png) |
(158) |
The prefactor in the definition of the current in the tight binding scheme (eq.(113)) is imaginary, but the evaluated current is real.