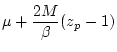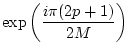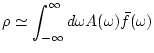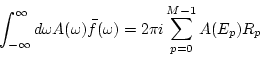�$B in the non-equilibrium
�$B>e$X�(B: in the equilibrium
�$BLa$k�(B: total charge from contour
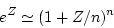 |
(84) |
then
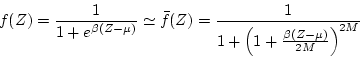 |
(85) |
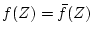 when
when
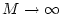
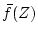 has poles at
has poles at
total charge is
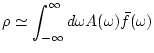 |
|
|
(88) |
From the counter integration of the upper-half plane,
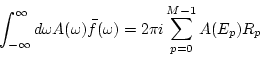 |
(89) |
where 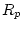 is residue and equals
is residue and equals 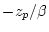 .
.
kino
�$BJ?@.�(B18�$BG/�(B4�$B7n�(B17�$BF|�(B
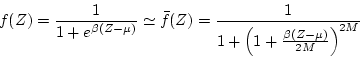
![]() has poles at
has poles at