


�$B total charge using modifed
�$B>e$X�(B: in the equilibrium
�$BLa$k�(B: total charge from contour
TRANSIESTA uses a different approach.
eq.(75) can be written as
where
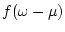 is the Fermi distribution function.
using the thermal Green function and the pole of
is the Fermi distribution function.
using the thermal Green function and the pole of 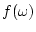 is at
is at 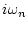 ,
,
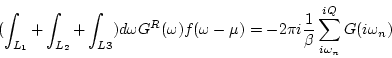 |
(82) |
where the path 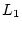 is (
is (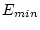 ,0)
,0) 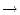 (
(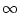 ,0),
,0), 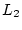 is (
is (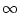 ,
,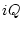 )
) 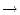 (
(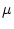 ,
,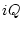 )
and
)
and 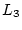 is (
is (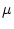 ,
,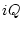 )
) 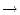 (
(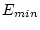 ,0).
,0).
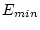 is smaller than the minimum of the eigenvalues.
is smaller than the minimum of the eigenvalues.
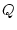 is a small value enough to stabilize the integration.
Then
is a small value enough to stabilize the integration.
Then
![\begin{displaymath}
\rho_{ij} = -\frac{1}{\pi} {\rm Im} \left[
\int_{L_2+L_3} d...
...\frac{1}{\beta} \sum_{i\omega _n}^{iQ} G(i\omega _n) \right]
\end{displaymath}](img199.png) |
(83) |
practical upper limit
to calculate
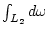 is
is 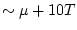 due to the presence of
due to the presence of
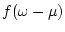
Note that 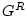 has no pole in the upper half plane of
has no pole in the upper half plane of 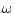



�$B total charge using modifed
�$B>e$X�(B: in the equilibrium
�$BLa$k�(B: total charge from contour
kino
�$BJ?@.�(B18�$BG/�(B4�$B7n�(B17�$BF|�(B
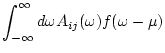
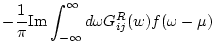
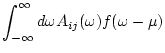
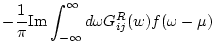
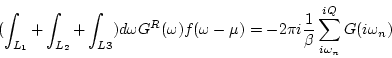
![]() has no pole in the upper half plane of
has no pole in the upper half plane of ![]()