Japanese/English


Ryo Tamura
website
|
Artificial intelligence can be used to design new molecules; it is becoming a popular tool because of its potential for discovering molecules in unexplored chemical spaces,
its ability to screen a huge number of potential molecules in a short amount of time and its tendency to find unconventional ways of solving problems.
However, whether such molecules can be actually synthesized and whether they display the desired functionalities in the real world is an open question.
we studied the de novo molecule generation by machine learning. We prepared AI-assisted chemistry platform for discovering new photo-functional molecules (Fig. 1). It consists of ChemTS (molecule generator)[1,2] and GAUSSIAN (DFT simulator)[3,4] and was configured to generate molecules whose first excited state is at desired wavelength. Among the molecules discovered, six were synthesized (Fig. 2) and five were confirmed to reproduce DFT predictions. This result shows the potential of AI-assisted chemistry to discover ready-to-synthesize novel molecules with modest computational resources. Thus, We believe that the potential is high for a transformative tool in chemistry[5]. 〈Press〉 The Nikkei (Aug. 24, 2018) Japan Metal Daily (Aug. 27, 2018, 3rd page) OPTRONICS ONLINE (Aug. 28, 2018) Nikkan Sangyo Shimbun (Aug. 28, 2018, 11th page) Nikkan Kogyo Shimbun (Aug. 29, 2018, 7th page) Chemical Daily (Aug. 29, 2018, 1st page) Electronic Device Industry News (Sept. 13, 2018) Dempa Shimbun (Sept. 14, 2018, 10th page) 〈References〉 [1] X. Yang, J. Zhang, K. Yoshizoe, K. Terayama, and K. Tsuda, Science and Technology of Advanced Materials 18 972 (2017). [2] https://github.com/tsudalab/ChemTS [3] R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules (Oxford University Press, 1989). [4] http://gaussian.com/ [5] M. Sumita, X. Yang, S. Ishihara, R. Tamura, and K. Tsuda, ACS Central Science 4, 1126 (2018). |
|
|
To accelerate an estimation of effective physical model[1],
an efficient method for finding a better maximizer of computationally extensive probability distributions is proposed on the basis of a Bayesian optimization technique.
Bayesian optimization has recently attracted much attention as a method to search the maximizer/minimizer of a black-box function in informatics and materials science[2].
In this method, the black-box function is interpolated by Gaussian processes,
and the interpolated function is used to predict the maximizer/minimizer of the black-box function.
A key idea of the proposed method is to use extreme values of acquisition functions by Gaussian processes for the next training phase,
which should be located near a local maximum or a global maximum of the probability distribution.
Our Bayesian optimization technique is applied to the posterior distribution in the effective physical model estimation[3]. Here, instead of searching the maximizer of posterior distribution (P), the minimizer of energy function defined by E = - log P is searched. Even when the number of sampling points on the posterior distributions is fixed to be small, the Bayesian optimization provides a better minimizer of the energy function in comparison to those by the random search method, the steepest descent method, or the Monte Carlo method(Fig. 1). In this demonstration, the quantum Heisenberg model is used as the target Hamiltonian and the temperature dependence of specific heat is inputted. Furthermore, the Bayesian optimization improves the results efficiently by combining the steepest descent method and thus it is a powerful tool to search for a better maximizer of computationally extensive probability distributions. Because the maximizer of a probability distribution is searched in many scientific fields, our method will play an important role in the promotion of science. 〈References〉 [1] R. Tamura and K. Hukushima, Phys. Rev. B 95 064407 (2017). [2] T. Ueno, T. D. Rhone, Z. Hou, T. Mizoguchi, and K. Tsuda, Materials Discovery 4, 18 (2016). [3] R. Tamura and K. Hukushima, PLoS ONE 13, e0193785 (2018). |
|
|
We showed that the nanomechanical sensing combined with machine learning realizes the specific information extraction, e.g. alcohol content quantification,
from the smells of liquors(Fig. 1).
Here, a newly developed nanomechanical sensor platform, a Membrane-type Surface stress Sensor (MSS)[1,2], was utilized.
We prepared multiple MSS coated with some sensing materials such as functional nanoparticles and polymers,
and then measured the smells of various types of alcohol, such as beer and vodka,
recording the electrical signal patterns specific to each type of alcohol.
We selected characteristic features from the measured signals
and kernel ridge regression[3] was used to predict the alcohol content of the samples,
resulting in successful alcohol content quantification.
Furthermore, we optimized sensing materials, based on the information obtained from machine learning.
Through such mutual optimization between hardware (the MSS and sensing materials) and software (the prediction model and the features),
we succeeded in accurately quantifying the alcohol contents of liquors (red wine, imo-shochu, and whisky) that were not used to train the prediction model(Fig. 2)[4].
The applicability of this data-driven nanomechanical sensing is not limited to the alcohol content quantification but to various fields including food, security, environment, and medicine. 〈Press〉 NIMS Press release (June 20, 2017) [Link] 47NEWS (June 20, 2017) MyNavi News (June 21, 2017), Nikkei Sangyo Shimbun (June 22, 2017, 8th page) EE Times Japan (June 27, 2017) Nikkan Kogyo Shimbun (June 28, 2017, 7th page) AI BIBLIO (June 28, 2017) Newswitch (June 29, 2017) Tsukuba Science News (June 30, 2017) The Science News (June 30, 2017, 4th page) Mainichi Shimbun (July 6, 2017, Evening paper, 10th page) Mainichi Shimbun (July 7, 2017, Ibaraki ver., 2nd page) Academist Journal (Sept. 5, 2017) Asahi Shimbun (Sept. 7, 2017, 25th page) 〈References〉 [1] G. Yoshikawa, T. Akiyama, S. Gautsch, P. Vettiger, and H. Rohrer, Nano Letters 11, 1044 (2011). [2] http://www.nims.go.jp/eng/news/press/2017/06/201706200.html. [3] C. M. Bishop, Pattern Recognition and Machine Learning (Springer-Verlag, New York, 2006). [4] K. Shiba, R. Tamura, G. Imamura, and G. Yoshikawa, Scientific Reports 7, 3661 (2017). |
|
|
The importance of data-driven techniques using machine learning[1, 2] is recognized in both academic and industrial fields.
Machine learning is generally a statistical tool used to extract the inherent structure from a finite set of observed data.
In the condensed matter physics, machine learning techniques have been used such as for interpolation of density-functional theory (DFT)[3] and for model selection[4]. We developed a method for estimating the effective model from a given physical quantity by the machine learning based on the Bayesian statistics(Fig.1). In the estimation method, plausible model parameters that explain the given physical quantity are determined by maximizing the posterior distribution. We suppose that, with the help of machine learning technique based on a sparse prior and cross validation, relevant terms are successfully selected from a candidate model Hamiltonian including redundant terms[5]. The efficiency of the estimation method was tested by using synthetic magnetization curve data obtained by the classical Heisenberg model. Our results show that the proposed method enables estimation of the model parameters in the spin Hamiltonian correctly. It should be emphasized that the framework of our estimation method can be used not only for magnetization curves but also for any measured data as the input data. 〈References〉 [1] T. M. Mitchell, Machine Learning (McGraw-Hill, New York, 1997). [2] C. M. Bishop, Pattern Recognition and Machine Learning (Springer-Verlag, New York, 2006). [3] T. Suzuki, R. Tamura, and T. Miyazaki, Int. J. Quantum Chem. 117, 33 (2017). [4] H. Takenaka, K. Nagata, T. Mizokawa, and M. Okada, J. Phys. Soc. Jpn. 83, 124706 (2014). [5] R. Tamura and K. Hukushima, Phys. Rev. B 95, 064407 (2017). |
|
|
Recently, machine learning has emerged as a powerful approach for predicting quantum-mechanical properties of molecules and solids[1-4].
In our study,
we traine a machine-learning model on a crystalline silicon system in order to directly predict the quantum mechanical forces at a wide range of temperatures using kernel ridge regression and atomic fingerprints representing local environments of atoms.
If we can quickly predict the quantum mechanical forces,
the molecular dynamics simulation with the very long time needed for the prediction of thermodynamic and kinetic properties can be performed. We provide a simple, intuitive prescription for training a robust machine learning force field that can be applicable to a range of temperatures. The our prescription is as follows: (i) We perform the molecular dynamics simulations based on density functional theory with the canonical ensemble at a much higher temperature (below the melting point). Training data is sampled by the random sampling into this molecular dynamics simulation. (ii) We construct the machine learning model for quantum mechanical forces by performing the kernel ridge regression. Here, the same form of the atomic finger print in Ref. [5] is used. With our trained machine learning model, the force prediction errors are about 2% or smaller with respect to the corresponding force ranges, in the temperature region between 300 and 1650 K (Fig. 1 is an example of 900K). We also verify the applicability to a larger system, ensuring the transferability with respect to system size[6]. 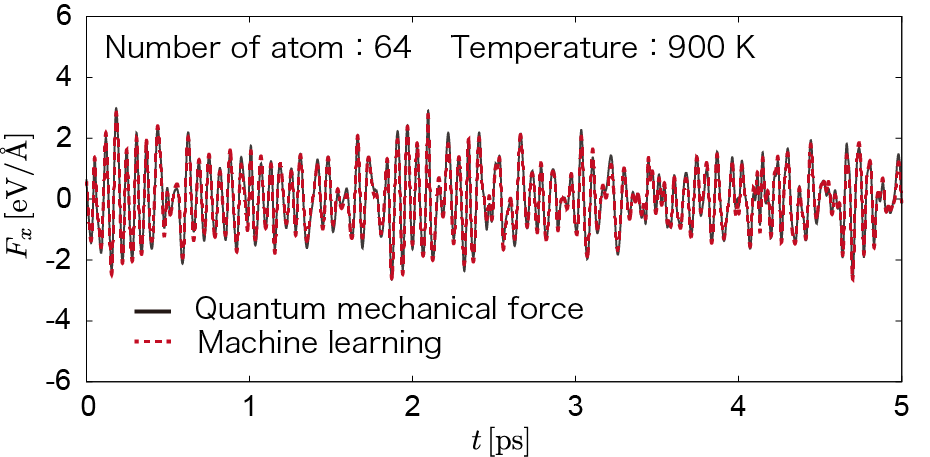 Fig. 1 〈References〉 [1] Z. Li, J. R. Kermode, and A. De Vita, Phys. Rev. Lett. 114, 096405 (2015). [2] M. Rupp, Int. J. Quantum Chem. 115, 1058 (2015). [3] A. Seko, A. Takahashi, and I. Tanaka, Phys. Rev. B 92, 054113 (2015). [4] T. Tadano and S. Tsuneyuki, Phys. Rev. B 92, 054301 (2015). [5] V. Botu and R. Ramprasad, Int. J. Quantum Chem. 115, 1074 (2015). [6] T. Suzuki, R. Tamura, and T. Miyazaki, Int. J. Quantum Chem. 117, 33 (2017). Our paper[6] was chosen as Cover Image in International Journal of Quantum Chemistry.  |
|
|
The magnetic refrigeration is a cooling technology using magnetic materials [1, 2].
When the magnetic field turned off in the isothermal process, the magnetic entropy increases in conventional ferromagnets and paramagnets.
According to the magnetic entropy change, the magnetic materials absorb an amount of heat from outside, which is called magnetocaloric effect (MCE).
In long time, it has been believed that ferromagnets are useful for magnetic refrigeration because a large magnetic entropy change is observed around the Curie temperature.
On the other hand,
recently,
MCEs in non-ferromagnetic materials were also investigated,
and thus the non-ferromagnetic material for magnetic refrigeration has been receiving a lot of attention. The purpose of this research is to clarify the relationship between magnetic ordered structure and MCE by Monte Carlo simulations based on the Wang-Lanudau method [3, 4]. Here, we investigated MCEs in the Ising models on a simple cubic lattice where the ground states are ferromagnetic, A-type, C-type, and G-type antiferromagnetic structures. As a result, in antiferromagnets, we found that the magnetic entropy reaches a maximum value at a finite magnetic field Hmax(T) when the temperature is fixed below the Neel temperature. Based on the fact, we proposed a protocol for applying magnetic fields (Fig. 1) to achieve the maximum efficiency for magnetic refrigeration in antiferromagnets where the magnetic field is varied from finite to Hmax(T) [5]. By using our proposed protocol, we showed that antiferromagnets exhibit a larger magnetic entropy change than ferromagnets below transition temperature. Furthermore, by using our proposed protocol, the entropy change, adiabatic temperature change, and cooling capacity are maximized in antiferromagnets [6]. Note that our proposed protocol for applying magnetic fields can be widely applied to not only antiferromagnets but also non-ferromagnetic materials to achieve a maximum efficiency for magnetic refrigeration. 〈Press〉 NIMS Press release (March 10, 2014) [Link] MyNavi News (Mar. 12, 2014) The Chemical Daily (Mar. 19, 2014, 8th page) The Science News (Mar. 28, 2014, 2nd page) Yano E plus (May 15, 2015) 〈References〉 [1] A. M. Tishin and Y. I. Spichkin, The Magnetocaloric Effect and its Applications (Taylor & Francis, London, 2003). [2] K. A. Gschneidner Jr., V. K. Pecharsky, and A. O. Tsokol, Rep. Prog. Phys. 68, 1479 (2005). [3] F. Wang and D. P. Landau, Phys. Rev. Lett. 86, 2050 (2001). [4] F. Wang and D. P. Landau, Phys. Rev. E 64, 056101 (2001). [5] R. Tamura, T. Ohno, and H. Kitazawa, Appl. Phys. Lett. 104, 052415 (2014). [6] R. Tamura, S. Tanaka, T. Ohno, and H. Kitazawa, J. Appl. Phys. 116, 053908 (2014). |
|
|
In the two-dimensional Heisenberg model with nearest-neighbor and third nearest-neighobr interactions, the order parameter space is SO(3)xC3 [1, 2, abstract].
In this model, the first-order phase transition with C3 symmetry breaking occurs at finite temperature.
Moreover, the Z2 vortex dissociation which comes from SO(3) symmetry occurs at the first-order phase transition temperature.
The purpose of this study is to clarify the phase transition nature of the three-dimensional system where the order parameter space is SO(3)xC3.
Then, we study the finite temperature properties of the frustrated Heisenberg model on a stacked triangular lattice by Monte Carlo simulations.
The model has three types of interactions: the nearest-neighbor and third nearest-neighbor interactions in each triangular layer and the interlayer interaction (Fig. 1).
In systems where the order parameter space is described by the direct product between two groups AxB, there are many possible scenarios for phase transition nature. For example, both A and B are simultaneously broken at the phase transition temperature, and successive phase transitions occur when A and B are successively broken. In our model, a first-order phase transition with breaking of SO(3) and C3 symmetries occurs at finite temperature [3].
Moreover, we calculate the interlayer-interaction dependence of energy histogram (Fig. 2).
As a result, we discover that the transition temperature increases but the latent heat decreases as increasing interlayer interaction (Fig. 2).
This behavior of latent heat is opposite to the behavior observed in typical unfrustrated three-dimensional systems [4, 5].
〈References〉 [1] R. Tamura and N. Kawashima, J. Phys. Soc. Jpn. 77, 103002 (2008). [2] R. Tamura and N. Kawashima, J. Phys. Soc. Jpn. 80, 074008 (2011). [3] R. Tamura and S. Tanaka, Phys. Rev. E 88, 052138 (2013). [4] F. Y. Wu, Rev. Mod. Phys. 54, 235 (1982). [5] Y. Kamiya, N. Kawashima, and C. D. Batista, Phys. Rev. B 84, 214429 (2011). |
|
|
The antiferromagnetic Heisenberg model on triangular lattice is the fundamental geometrically frustrated magnet.
In the model, since a phase transition associated with long-range order of spin is prohibited by the Mermin-Wagner theorem, topological defect plays an important role.
If only nearest-neighbor interactions J1 exist, by dissociating Z2 vortices which comes from the order parameter space SO(3), a topological phase transition occurs [1].
Furthermore, by adding third nearest-neighbor interaction J3, the order parameter space becomes SO(3)xC3, and the first-order phase transition with C3 symmetry breaking and the Z2 vortex dissociation simultaneously occur [2, 3, abstract].
However, a second-order phase transition has never been discovered in longstanding studies on Heisenberg models on triangular lattice.
We study finite-temperature properties of the Heisenberg model on a distorted triangular lattice with nearest-neighbor interaction J1 and third nearest-neighbor interaction J3 where the order parameter space is SO(3)xZ2 [4].
The ground state spin configuration where the Z2 symmetry is broken is shown in Fig. 1.
By Monte Carlo simulations, we find a second-order phase transition with Z2 symmetry breaking which belongs to the universality class of two-dimensional Ising model (Fig. 2).
Moreover, we confirm that Z2 vortices dissociate at the second-order phase transition point.
To our knowledge, our study is the first example that shows a Z2 vortex dissociation at the critical point.
〈References〉 [1] H. Kawamura and S. Miyashita, J. Phys. Soc. Jpn. 53, 4138 (1984). [2] R. Tamura and N. Kawashima, J. Phys. Soc. Jpn. 77, 103002 (2008). [3] R. Tamura and N. Kawashima, J. Phys. Soc. Jpn. 80, 074008 (2011). [4] R. Tamura, S. Tanaka, and N. Kawashima, Physical Review B 87, 214401 (2013). Our paper[4] was chosen as Kaleidoscope in Physical Review B. 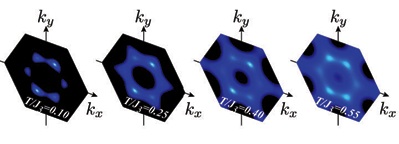 |
|
|
The infinite-layer iron oxide SrFeO2 was synthesized by hydride reduction of SrFeO3 which has the perovskite structure [1].
This material exhibits (πππ) order with a high Neel temperature TN = 473 K.
The random magnet Sr(Fe1-xMnx)O2 was synthesized by substituting
Mn ion for Fe ion in SrFeO2 [2].
In Sr(Fe1-xMnx)O2 for x = 0.3,
it was observed that the simultaneous appearance of (πππ) and (ππ0) wave vectors at finite temperature in neutron scattering measurement.
Inspired by this experimental results of random magnet Sr(Fe1-xMnx)O2, we investigated the ground state and finite-temperature properties of the classical site random Heisenberg model on the cubic lattice with competed interlayer couplings [3, 4]. We obtained the phase diagram of temperature versus concentration of Mn ions x (see Fig. 1). In this model, we found the novel magnetic structure called “random fan-out state” (see Fig. 2). This spin structure explains the simultaneous appearance of (πππ) and (ππ0) wave vectors. Since the Rietveld analysis assuming the random fan-out state agrees well with the neutron diffraction pattern of Sr(Fe0.7Mn0.3)O2, we concluded that the random fan-out state is reasonable for the spin-ordering pattern of Sr(Fe0.7Mn0.3)O2 in the low-temperature phase. 〈References〉 [1] L. Seinberg, T. Yamamoto, C. Tassel, Y. Kobayashi, N. Hayashi, A. Kitada, Y. Sumida, T. Watanabe, M. Nishi, K. Ohoyama, K. Yoshimura, M. Takano, W. Paulus, and H. Kageyama, Inorg. Chem. 50, 3988 (2011). [2] Y. Tsujimoto, C. Tassel, N. Hayashi, T. Watanabe, H. Kageyama, K. Yoshimura, M. Takano, M. Ceretti, C. Ritter, and W. Paulus, Nature 450, 1062 (2007). [3] R. Tamura and N. Kawashima, J. Phys.: Conf. Ser. 320, 012013 (2011). [4] R. Tamura, N. Kawashima, T. Yamamoto, C. Tassel, and H. Kageyama, Phys. Rev. B 84, 214408 (2011). Our paper[4] was chosen as Kaleidoscope in Physical Review B. 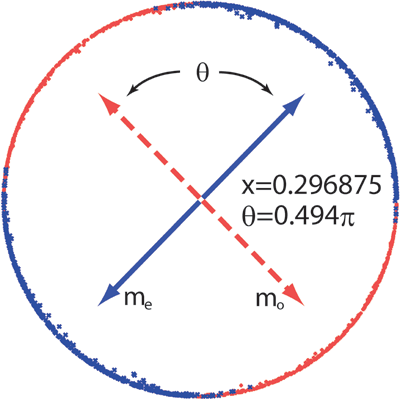 |
|
In order to analyze the phase transition with breaking of q-fold symmetry,
it is enough to consider the ferromagnetic q-state Potts model in many circumstances [1, 2].
Indeed, Potts model has succeeded in analysis of a phase transition with discrete symmetry breaking in experimental and theoretical systems.
However, some counterexamples were found, e.g. a first-order phase transition with breaking of threefold symmetry occurs in two-dimensional frustrated spin systems [3, 4].
This is because a second-order phase transition takes place at finite temperature in the standard q-state ferromagnetic Potts model on two-dimensional lattice for q=2, 3, and 4.
In these systems, it can be regarded that there are some kinds of degrees of freedom in addition to discrete q states because of peculiar density of states.
We expected that these extra degrees of freedom affect the nature of phase transition.
To consider this situation for simplicity, we invented the ferromagnetic Potts model with invisible states that are added as redundant states.
The model Hamiltonian is given as 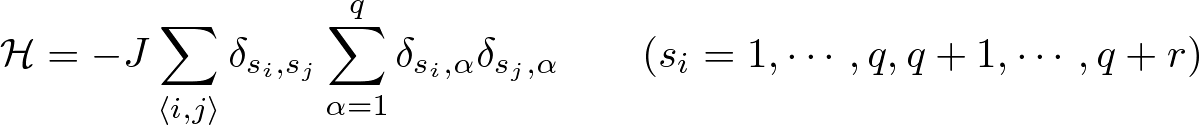 . .We investigated nature of phase transition in this model by mean-field calculation and Monte Carlo simulation and confirmed our present model on two-dimensional lattice (q=2, 3, and 4) undergoes a first-order phase transition with spontaneous q-fold symmetry breaking due to entropy effect of invisible states (see Fig. 1) [5, 6]. We obtained phase transition temperature and latent heat for some parameter sets (see Tab. 1). Furthermore, we found that there is a two-step relaxation which is typical behavior in systems which exhibit a first-order phase transition in analysis of dynamic properties [7]. Thus, this model is expected to be a fundamental model for analyzing a first-order phase transition with spontaneous discrete symmetry breaking. To change order of phase transition is an important topic for not only statistical physics but also information science (especially, quantum annealing or quantum adiabatice computation). Thus, this method to change order of phase transition is expected to be an efficient tool to solve optimization problems [8, 9]. 〈References〉 [1] R. B. Potts, Proc. Camb. Phil. Soc. 48, 106 (1952). [2] F. Y. Wu, Rev. Mod. Phys. 54, 235 (1982). [3] R. Tamura and N. Kawashima, J. Phys. Soc. Jpn. 77, 103002 (2008). [4] E. M. Stoudenmire, S. Trebst, and L. Balents, Phys. Rev. B 79, 214436 (2009). [5] R. Tamura, S. Tanaka, and N. Kawashima, Prog. Theor. Phys. 124, 381 (2010). [6] S. Tanaka, R. Tamura, and N. Kawashima, J. Phys.: Conf. Ser. 297, 012022 (2011). [7] S. Tanaka and R. Tamura, J. Phys.: Conf. Ser. 320, 012025 (2011). [8] S. Tanaka, R. Tamura, I. Sato, and K. Kurihara, Kinki University Series on Quantum Computing Volume 5, pp. 169-192 (World Scientific, 2012). [9] R. Tamura, S. Tanaka, and N. Kawashima, Kinki University Series on Quantum Computing Volume 7, pp. 217-238 (World Scientific, 2012). |
|
|
The chalcogenide insulator NiGa2S4 is the frustrated magnetic material having triangular lattice.
The magnetic layer of Ni ions (S = 1) forms an almost perfectly equilateral triangular
lattice.
In this material,
it was observed that the incommensurate short-range ordered state which is described by characteristic wave vector k = (1.896π/3, 0) appears at 1.5 K.
In mean-field calculation,
this wave vector can be explained by competition between ferromagnetic nearest-neighbor interaction J1 and antiferromagnetic third nearest-neighbor interaction J3.
Inspired by the interesting properties and characteristic interactions of triangular magnet NiGa2S4 [1, 2], we investigated the ground-state and finite-temperature properties of the classical Heisenberg model on the triangular lattice with ferromagnetic nearest-neighbor interaction J1 and antiferromagnetic third nearest-neighbor interaction J3 [3, 4]. In the range of -4 < J1/J3 < 0, the ground state of this model is spiral spin state breaking discrete lattice rotation symmetry (see Fig. 1) induced by the competition between a number of interactions. From Monte Carlo simulations, we obtained the clear evidence of the occurrence of the first-order phase transition at finite temperature in the thermodynamic limit (see Fig. 2). Moreover, we investigated about the Z2 vortex dissociation [5] and the discrete symmetry breaking relating to the ground-state properties. We concluded that the dissociation of Z2 vortex pairs and the breaking of discrete lattice rotation symmetry occur at the first-order phase transition temperature. Furthermore, we confirmed that the second-order phase transition occurs in our model on a "distorted" triangular lattice [6, abstract], and also the first-order phase transition occurs in our system with stacked interactions [7, abstract]. 〈References〉 [1] S. Nakatsuji, Y. Nambu, H. Tonomura, O. Sakai, S. Jonas, C. Broholm, H. Tsunetsugu, Y. Qiu, and Y. Maeno, Science 309, 1697 (2005). [2] S. Nakatsuji, Y. Nambu, K. Onuma, S. Jonas, C. Broholm, and Y. Maeno, J.Phys: Condens. Matter 19, 145232 (2007). [3] R. Tamura and N. Kawashima, J. Phys. Soc. Jpn. 77, 103002 (2008). [4] R. Tamura and N. Kawashima, J. Phys. Soc. Jpn. 80, 074008 (2011). [5] H. Kawamura and S. Miyashita, J. Phys. Soc. Jpn. 53, 4138 (1984). [6] R. Tamura, S. Tanaka, and N. Kawashima, Physical Review B 87, 214401 (2013). [7] R. Tamura and S. Tanaka, Phys. Rev. E 88, 052138 (2013). |
|